1.数学符号的功能

在世界上能不分国家和种族都适用的文字，只有惟一的数学符号。当您用数学符号写出一个运算或推理过程的时候，如：

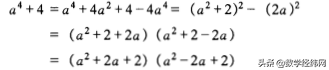
任何国家只要念过初中的人都会明白无误地懂得它所表达的意思。

数学能以现在的这种表示简明、结构优美的形式出现，首先得要感谢数学记号和符号体系的出现，它对数学的发展和推动作用是极其巨大的。德国数学家莱布尼茨说过：”符号的巧妙和符号的艺术，是人们绝妙的助手，因为它们使思考工作得到节约。在这里它以惊人的形式节省了思维。”俄国数学家罗巴切夫斯基说：”数学符号的语言更加完善、准确明了地提供了把一些概念传达给别人的方法。利用了符号，数学上的每一个论断和它所描述的东西就可以更快地被别人所了解。”

数学符号的重要性日益被人们所认识，而了解数学符号的创造历史，就显得很有意义了。

2.数学符号的使用

早在公元前6世纪，印度所首创的1，2，3，…，9以及以后的0的数字记号，为数字的书写和运算带来了极大的方便。而现在我们十分熟悉的”+”、”-”、”×”、”÷”、”=”等一系列符号，则是在数学家经过了一千年的探索后才逐渐出现的，下面谈谈数学符号使用的历史：

加法符号”+”：1489年德国数学家魏德曼开始在他所著的数学书中首先使用。但直到16世纪之后，经过德国数学家韦达的提倡和宣传，加号才开始普及。

减法符号”-”：仍是德国数学家魏德曼1489年在他的著作中首先使用，但直到1630年，”-”号才获得大家的公认。

乘法符号”×”：英国数学家奥特雷德于1631年在他的著作中提出用”×”表示乘法。但莱布尼茨赞成用”• ”表示相乘。”×”与”• ”相持不下，一直到今天，这两种运算符号都继续使用着。

除法符号”÷”：英国数学家奥屈特1631年曾经用”：”表示”除”或”比”，1684年莱布尼茨也曾提出用”：”表示”除”。当时也有人主张用除线”—”表示相除(如)。1659年瑞士的拉恩把两种除号合二为一，得到了我们所熟悉的除法符号”÷”。

等于号”=”：1540年英国数学家雷科德开始使用”=”作为等号，他认为”最相像的两件东西莫过于两条平行线”。但直到17世纪以后，”=”才真正被大家普遍使用。

小括号” ( ) ”、中括号” [ ] ”、大括号” { } ”：小括号” ( ) ”或称圆括号是1544年出现的；中括号” [ ] ”或称方括号，大括号” { } ”或称花括号都是1593年由数学家韦达引入的。

大于号”＞”和小于号”＜”：1631年由美国代数学家哈里奥特首创。

近似号”≈”和全等号”≌”：17世纪由莱布尼茨开始使用。

根号”√”：由法国数学家笛卡儿在17世纪初开始使用。

指数符号”an”：用指数来表示数或式的乘幂，经过了复杂的演变过程。从14世纪时法国的奥利森、1484年法国的舒开、1637年笛卡儿直到1801年由法国著名数学家高斯用x²代替xx，而较高的幂指数x³，x⁴等是笛卡儿开始引用的，但没有用xn，直到著名数学家牛顿指出不论什么指数都用an来表示。

对数符号”log、ln”：对数符号”log”是”Logarithm(对数)”的缩写，进一步缩写”lg”表示以10为底的对数即常用对数。如果以无理数e为底（e=2.71828…)，则称为自然对数，常用符号”ln”来表示。对数符号由德国数学家开普勒于1624年首创。

从16世纪起，经过了300年的实践和筛选，才使数学有了一个简洁明了的符号体系，把数学家从冗繁的文字叙述中解脱出来。这种数学的”文字”到19世纪已通行于全世界，不但推动了数学本身的发展，而且对其他学科的发展有着十分巨大的作用。

3.数学符号的分类和特点

a.数学符号通常可分为四种

象形符号：用符号形状特征来反映数学概念的符号，如平面图形符号：∠(角）、⌒(弧)、△(三角形）、▱(平行四边形）等是原图形的压缩象形；

关系符号：”=”、”≠”、”≡”、”≌”、”≈”、”＞”、”≤”、”∈””⊆”等是原型的改造符号；

缩写符号：是由数学概念的外文词汇的前一个或数个字母构成的缩写。如f表示函数（function)，R表示实数集(realnumber)，lim表示极限（limit)，其他如log表示对数，max表示最大值，min表示最小值，Σ表示和等。

约定符号：如x，y，z表示未知数，用a，b，c表示三角形的三边，用大写字母表示点，用小写字母表示线段或直线，用小写希腊字母α、β、γ表示平面，用”+、-、×、÷”表示四则运算等，都是人为的约定。

b.数学符号的特点

高度的概括性：自然语言本身就是一种概括，而数学语言又是对自然语言的进一步概括。如”0，1，2，3，…”用自然语言表示就是”一切自然数”，而用数学语言表示就是”N”。这样大大缩短了句子的长度，相应地增加了思维的进度，这就显露了数学的”简洁美”和”思维美”。

精确性：数学中每一个符号或由符号组成的式子只包含一个意思。如”+”、”π”、“lg”、“l0℃≤t≤20℃”等等都表示特定的含义，不能随便乱用。

形式化：数学符号把数学概念进行抽象，形成一种固定的程式。如函数用”y=f(x)”表示，一元二次方程用”ax2+bx+c=0，(a≠0)”表示，圆方程用”（x-a)²+(y-b)²=R2”表示等。

4.最奇特的数字系统

在所有的数字系统中，最奇特的一种是公元初中美洲玛雅人使用的数字。它与其他计数方式都不相同，它采用的二十进位制，但只有三个符号，即点”·”、划”—”和卵形就可以写出任何的数了。

用点、划可表示出1~19的自然数：

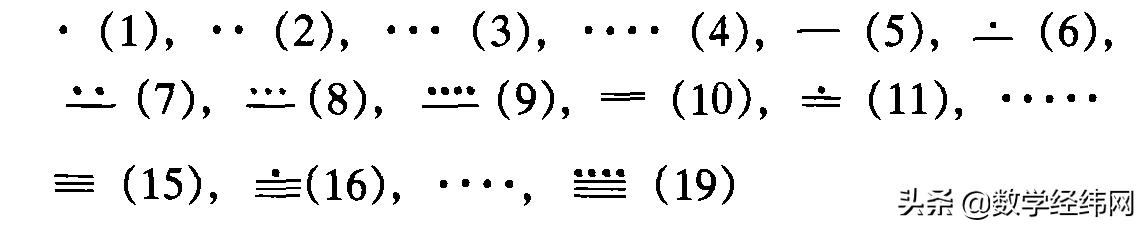
在任何数的下方加一个卵形，就把这个数扩大到20倍，如

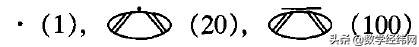
但他们在计算时，作了新规定：在一个数的下方加上第二个卵形后，原数不是乘以20，而是乘以18，例如

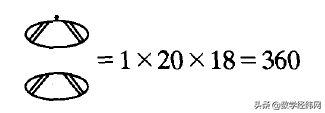
我们只需联想一下，一年正好是360天，就会理解他们为什么会做这样奇特的规定了。

5.”修养”中的符号和用符号表达的世界观

a.”修养”中的符号

名利面前不用”+”；困难面前不用”-”;

朋友之间不用”÷”；谈恋爱不用”△”;

守纪律不用”≈”；功劳和报酬之间不用”=”。

b.用符号表达的世界观

”+”号用在学习上；”-”号用在休息上；

”×”号用在工作上；”÷”号用在专业上；

”，”号用在委屈上；”!”号用在时间上；

”?”号用在成绩上；”=”号用在群众上；

”()”号用在创作上；”……”号用在事业上；

”→”号用在未来上。

数学符号的产生和使用，给数学谱写了无数美妙的乐章，给人类带来了巨大的财富。某著名科学家曾说：”大自然是以数的语言在讲话。”这些数字符号就是数学语言的词汇，它是数学家长期创作的数学语言中的精华，它比世界上任何一种语言更精练、更准确。数学家们关于数学符号的创作性劳动闪烁着人类的智慧和劳动结晶的光芒，也是对人类语言学的丰富和发展。