初中数学
《平面直角坐标系》
▶来源:人教版初中数学七年级下册第七章7.1.2《平面直角坐标系》教学建议:
1 在有序数对的基础上让学生思考如何表示一个有序数对(通过用数轴表示数进行引导)。
2 明确平面直角坐标系两条坐标轴的位置关系(垂直)以及各部分名称。
3 通过让学生自己根据坐标找点的位置以及根据位置找坐标总结出点的坐标与位置的关系。
有关资料:平面直角坐标系是在已经了解了有序数对的情况下进一步展开学习的,要求学生能够掌握根据点的坐标找到该点位置以及根据平面直角坐标系中的点找到该点坐标。本节内容为后续的函数乃至高中的解析几何等内容打下了基础,是代数与几何衔接的桥梁。
平面直角坐标系 教案
一、教学目标
【知识与技能】
掌握什么是平面直角坐标系,会通过点的坐标找到位置以及通过位置写出点的坐标。
【过程与方法】
在探索平面直角坐标系以及点的坐标与位置关系时,提升逻辑推理能力以及几何直观。
【情感态度价值观】
在自主探索中感受到成功的喜悦,激发学习数学的兴趣。
二、教学重难点
【教学重点】
掌握什么是平面直角坐标系。
【教学难点】
理解两个轴为何垂直,会通过点的坐标找到位置以及通过位置写出点的坐标。
三、教学过程
(一)引入新课
复习提问:什么是有序数对?能否举一个例子。
根据学生回答追问:有序数对所表示的位置如何直观表示?
(二)探索新知
总结学生回答:利用学过用数轴表示数,对于有序数对有两个数进而转到用两个数轴。进一步追问:用两个什么样的数轴?
让学生根据上节课举的电影院的例子对比座位行列是互相垂直的,自主探索得出结论:用相互垂直的两条数轴。
教师总结:由平面内两条互相垂直、原点重合的数轴组成平面直角坐标系,水平的数轴称为x轴或横轴,取向右为正方向;竖直的数轴称为y轴或纵轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点。
在黑板画出一个平面直角坐标系,并在其中点出A,B两个点,提问:点A如何用有序数对表示?
学生回答,教师总结:一个点的横坐标就是点向x轴做垂线垂足的坐标,纵坐标就是向
y轴做垂线垂足的坐标。
学生活动:写出B点的坐标。
(三)课堂练习
找出课前同学举例的有序数对(-2,-1),(-1,1)在平面直角坐标系的什么位置。
(四)小结作业
教师提问:今天有何收获?
引导学生总结:什么是平面直角坐标系,如何根据坐标找点,如何根据点找坐标。课后作业:思考平面直角坐标系中不同位置的点的坐标有何特点?
四、板书设计

五、教学反思
高中数学
《平面与平面垂直的性质》
▶来源:人教A版高中数学必修2-2.3.4-《平面与平面垂直的性质》教学建议:
1 可以把课前思考的两个问题拆成两部分使用,思考题的第二个探究长方体侧棱和底面是否垂直的问题可以在导入阶段使用;思考题的第一个画出黑板中的一条直线使之垂直于地面可以放在新授的环节之后,让学生进行巩固,也能进一步的发展学生的空间观念(并不能直观看到黑板中的直线与黑板和地面的交线垂直)。
2 导入后设计学生自主探究环节:引导学生将课堂导入的问题转化为直线垂直于平面内两条相交直线的问题进行求证。
3 可以进一步提升学生对于定理的认识,根据时间安排可选取以下两种方式:明确如果过一点有两条直线与平面垂直那么这两条直线重合;或者也可采用练习的方式加深学生的理解,鉴于至此空间中点线面的位置关系已全部讲解完毕,可以使用相对综合的位置关系分辨类题目进行提升,如教材中所给的例5。
4 由于本节内容相对复杂,故给出时间安排的建议:
使用思考题第二题进行引入,引导学生自主求证,教师将证明过程以及结论进行板书至此约用时6分钟,如面对10分钟试讲则练习采用思考题第一题;如面对15分钟试讲则练习采用讲解。如果过一点有两条直线与平面垂直那么这两条直线重合或附录例5两个练习二选一的方式。有关资料:在空间图形问题中可以通过直线与平面垂直判定平面与平面垂直。平面与平面垂直的性质
定理说明,由平面与平面垂直可以得到直线与平面垂直。这种直线与平面的位置关系同平面与平面的位置关系的相互转化,是解决空间图形问题重要的思想方法。在授课时可以适当强调本节内容的重要性。
附:例5:如图2.3-22,已知平面, 直线a满足 ,a ,a ,试判断直线a和平面 的位置关系。
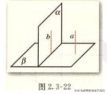
解:在 内做垂直于 与 交线的直线b,因为 ,所以b 。因为 ,所以a∥b。又因为a ,所以a∥ ,即直线a与平面平行
平面于平面垂直的性质 教案
一、教学目标
【知识与技能】
掌握平面与平面垂直的性质,会根据面面垂直证明线面垂直。
【过程与方法】
在探索证明平面与平面垂直的性质时,提升逻辑推理能力以及空间观念。
【情感态度价值观】
在自主探索中感受到成功的喜悦,激发学习数学的兴趣。
二、教学重难点
【教学重点】
掌握平面与平面垂直的性质。
【教学难点】
会根据面面垂直证明线面垂直。
三、教学过程
(一)引入新课
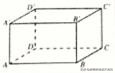
如图所示,长方体ABCD-A’B’C’D’中,平面A’ADD’与平面ABCD垂直,直线A’A垂直于其交线AD。平面A’ADD’内的直线A’A与平面ABCD垂直吗?
(二)探索新知
学生自主探索,抽取出问题模型,教师总结学生证明并板书:
如图所示,设α⊥β,α∩β=CD,AB⊂α,AB⊥CD,AB∩CD=B,讨论直线AB
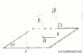
与平面β的位置关系。
在β内引直线BE⊥CD,垂足为B,则∠ABE是二面角α-CD-β的平面角,由α⊥β可知,AB⊥BE,又AB⊥CD,BE与CD是β内的两条相交直线,所以AB⊥β。
一般地,我们得到平面与平面垂直的性质定理。
两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
(三)课堂练习
例1:把黑板看成一个平面,它和地面所在的平面是垂直的。那么能不能在黑板上画一条和地而垂直的直线?是什么样的?
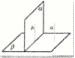
例2:如图,已知平面α,β,直线a满足α⊥β,a⊥β,a⊄α,试判断直线a和平面α的位置关系。
(四)小结作业
教师提问:今天有何收获?
引导学生总结:平面与平面垂直的性质定理
课后作业:将教室转化为一个长方体,用今天课上的知识证明一组线面垂直
四、板书设计

五、教学反思
