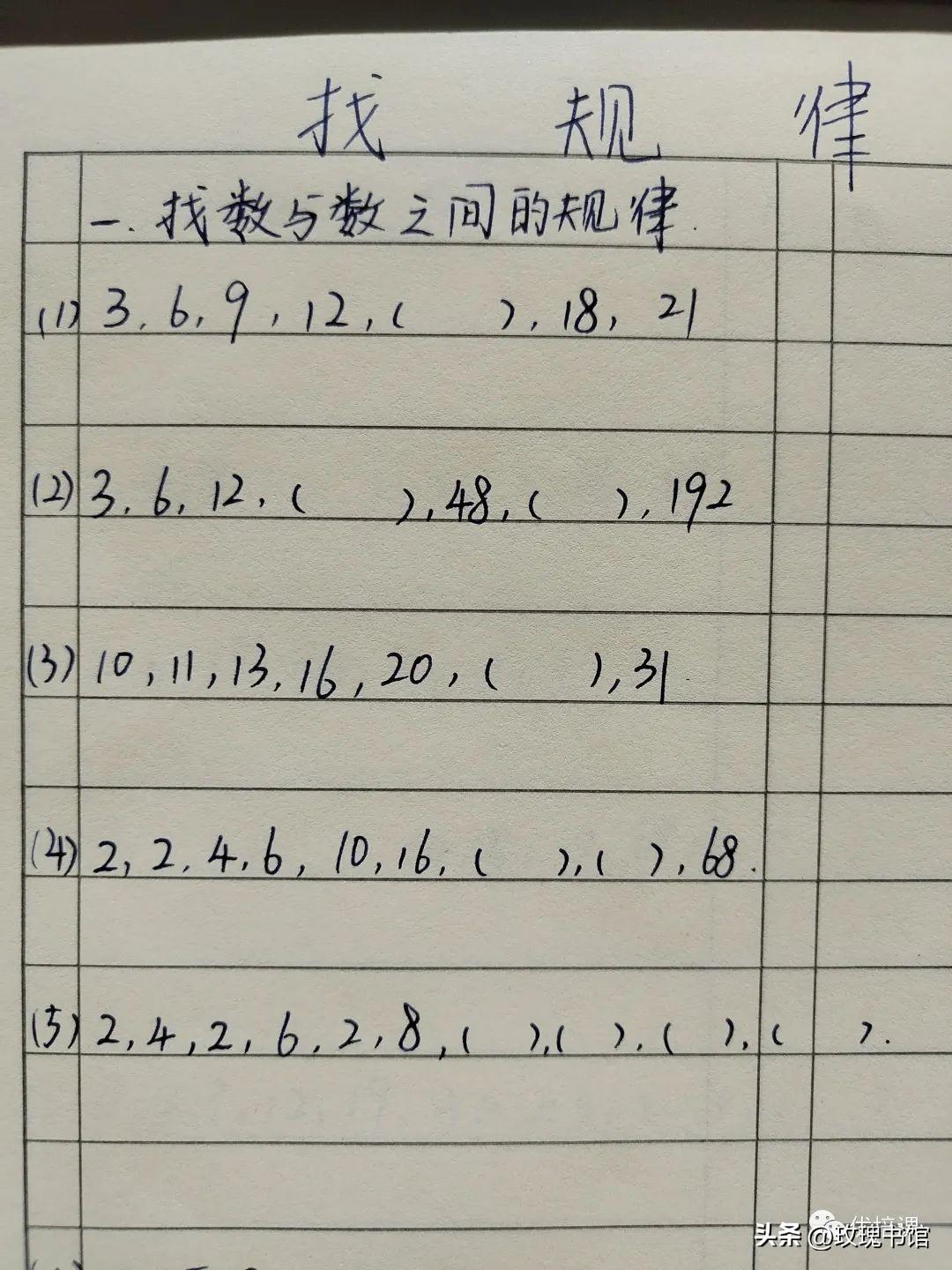
比如说:仔细观察,找出规律再填数
1.1,6,7,12,13,( ),( )
2.1,2,3,4,5,12,7,48,9,( ),( )
如果不开动脑筋的话,其实还是有一定难度的。
这种找规律的题一般分为三大类:

一、探索数与数之间的规律
1. 规律蕴含在相邻两个数的差或倍数中
如:1,2,3,4,5,( 6)……
这个的解题方法就是相邻两个数相差1
1,2,4,8,(16),(32)……
这个的规律就是相邻两个数为倍数关系,后一个数是前一个数的两倍
练习:找出下列数排列的规律,在括号内填上合适的数
如图所示:
2. 前后几个数为一组,以组为单位找关系
如:10,11,13,16,20,( ),( )
你能从这组数中找到什么规律呢?
仔细观察,你会发现前面几个数相邻的两数的差依次是1,2 ,3,4,对吧?
那么这个规律就是,前后相邻两数的差依次加1,所以答案就是:25,31
3. 需要将给出的数组分解通过对比发现规律
比如:2,4,2,6,2,8( ),( ),( ),( )
仔细观察,我们发现单数上都是2,双数上则是2的倍数,所以要以组来找规律。
即:2,4一组,2,6一组,2,8一组。
再找双数上的规律,发现依次+2,所以答案就是:2,10,2,12。
你填对了吗?

练习:
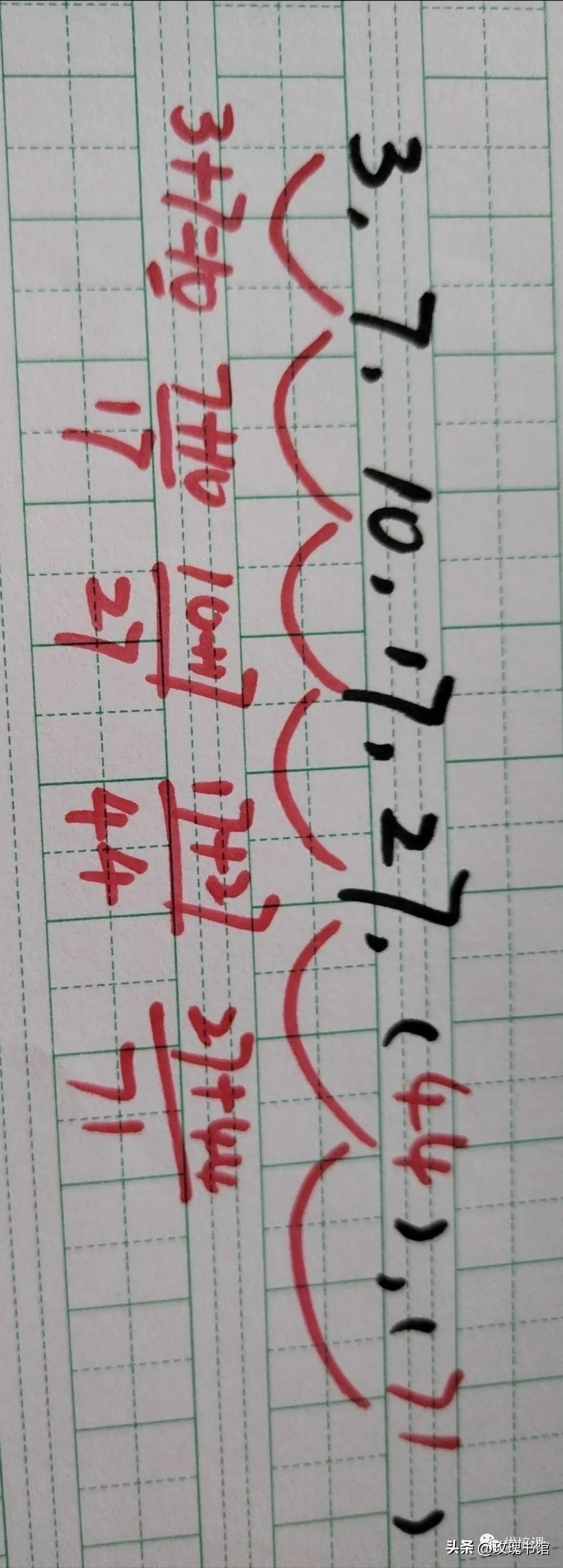
3,7,10,17,27,( ),( )
就算告诉你考点,我们也是要费点时间和精力才能算出来,何况孩子?
所以要想数学好,离不开平时的练,考试的时候可没那么多时间给他们去想。
但练过同类型的题后,他们就有思路了,再遇到也就不怕了。
那么这道题,大家算出来了吗?
哈哈,每天一道题,锻炼下脑,告别老年痴呆啊。
详解,请看下图,还是有点费脑壳。
4. 相邻两数的关系中,隐含着规律
如:2,5,8,( )
这道题简单吧,就是前后两个数相差3。
练习:( ),( ),10,5,12,6,14,7
看看算的对不对:
8,4
二、探索算式之间的规律
找规律的题型中还有一种,是根据算式的结果找规律。
比如:11×11=121,12×11=132,13×11=143,
14×11=( ),15×11=( ),16×11=( ),
43×11=( ),68×11=( )
又是一道难题。
它们之间有什么规律呢?
详解请看下图。

这个方法有点复杂了,其实简单点就是:把第一个数的十位数和个位数分别作为结果的百位和个位,中间那个数是个位数+十位数的和。
三、探索图形的变化规律
做这种题要首先找到图片中哪些部分发生了变化,
是按照什么规律变化的,
然后通过各部分的变化规律直接利用规律来找到答案。
比如下图:
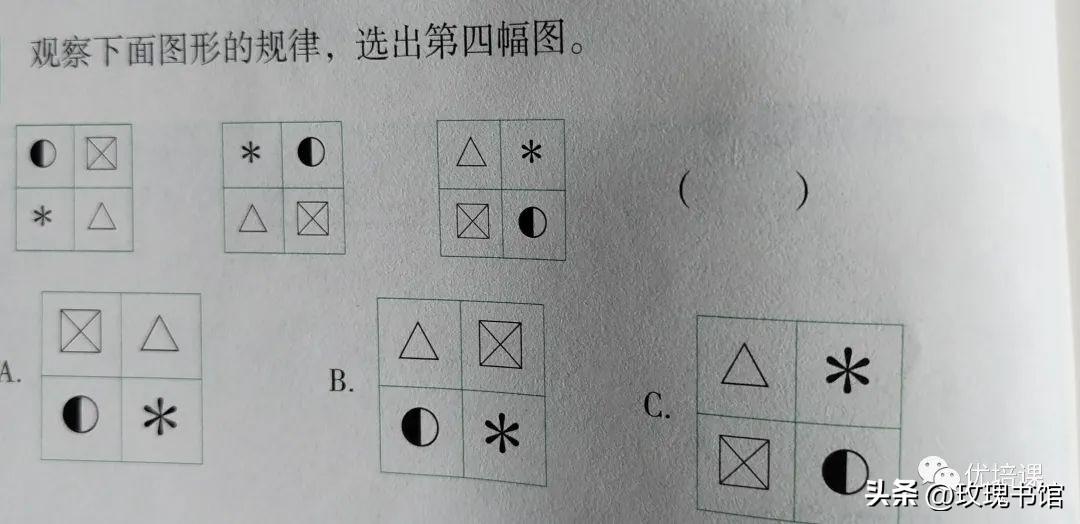
你发现它的变化规律了吗?
从第一幅图到第二幅图发生了哪些变化?怎么从第一幅图变成第二幅图的?找到规律后,再用第二幅图和第三幅图来验证是否正确。
从第一幅图到第二幅图,我们可以看到黑白的圆圈往右移动了一格,方框里的四幅图分别都向右移动了一格,我们按照这个规律发现第三幅图也是。
所以答案是A。
再来看下面这幅图,我感觉有一点点难度,如果没找到规律的话,确实不好做。
有兴趣的,可以自己做做看。

其实小学奥数里面有一个特点,就是它会提前学一些内容,但是用现在的知识也能解,只是稍微要费劲一点。
比如说找规律的时候,里面就有拓展的数学知识,应该是初中才学的——等差数列和等比数列。
等差数列就是从第二个数起,每一个数与前一个数的差都相等的数列。
比如:1,3,5,7,9
每个相邻数之间相差都是2。
上一题的答案如下图:
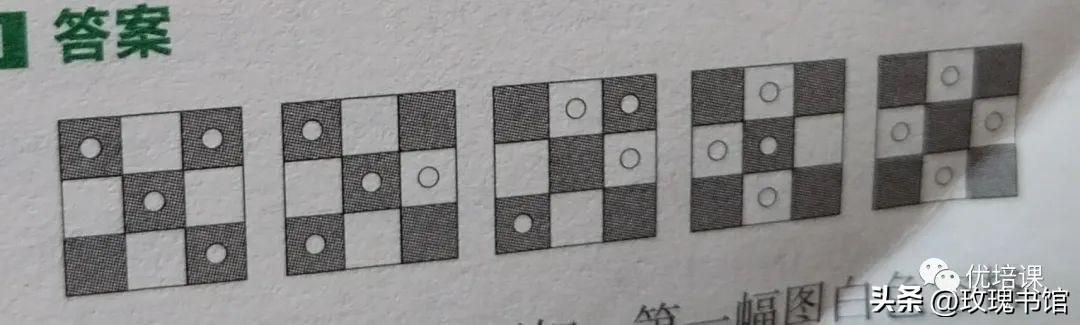
第一幅图,白色空格子里一个圆圈都没有,第二幅图白色格子里有一个圆圈,第三幅图白色格子里有两个,第四幅图,白色格子里有三个圆圈,那么第五个白色盒子里应该有四个。
你做对了吗?
再看看等差、等比数列。

等比数列就是从第二个数起,每一个数与前一个数的比都相等的数列。
比如:3,6,12,24,48
后一个数与前一个数的商是2。
再难一点,可能会考等差数列的一些规律,比如:
项数=(末项—首项)÷公差+1
首项=末项—(项数—1)×公差
……
但现阶段,对小学生来说,不做要求,不过培养孩子数学思维还是可以的,让他们多动脑,养成勤于思考的习惯。
而且很有挑战性,也可以培养他们的兴趣。
要知道北大“韦神”,从小就是以做数学为乐的。

感兴趣的家长可以让孩子做做这些题:
从1+2+3+4+5+……+100,结果等于多少?
一个等差数列:1,5,9,13,17,21,……它的第1000项等于多少?
你知道答案是多少吗?
可以试试哦。
