《数与形》教学设计
教学目标:
1.通过观察、计算和分析,能在形中找到数的规律;也能在数中找到与之对应的形。
2.经历探究数与形的全过程,在探究过程中进一步感知数形结合的思想。
3.引导学生感受以形表数的直观性和以数释形的规律性,体会数形结合思想在解决问题中的优越性。
教学重难点:
重点:发现数与形中隐藏的规律,理解数与形之间的对应关系,感知数形结合的思想,并体会其优越性。
难点:利用数形结合的思想解决问题。
教学过程:
一、谈话引入,揭示主题
师:在前面的学习中,我们常常跟数、形打交道。那大家有没有经历过用数形相结合来解决问题呢?现在让我们穿越时空去看一看。
(出示微课:一年级9+7=16通过小棒来解决,三年级四分之一加四分之三借用正方形来进行计算,四年级的植树问题)
师:其实,数形相结合思想对我们来说并不陌生,它一直贯穿于我们数学学习之中。著名的数学家华罗庚先生就曾经说过这样一段话:“数缺形时少直觉,形缺数时难入微,数形结合百般好,隔离分家万事休。”(课件出示)
师:我们全班一起读一遍。
师:数形结合百般好,好在哪呢?这节课,我们就一起走进数学广角---数与形(板书课题),来探索其中的奥秘。
二、活动体验,解决问题
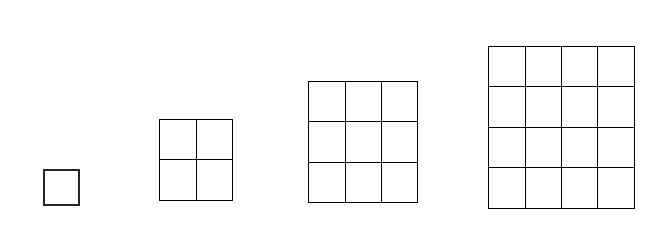
师:观察这些图形,各有多少个小正方形?用数或算式表示出来。将结果写在你的任务单上。
师:有些同学写出了一种或几种,请再思考下,能不能从不同的角度写出其他的表示方法呢?(找3个同学将答案写在黑板上)
生1:1,4,9,16
生2:1,22,32,42
生3:1,1+3,1+3+5,1+3+5+7
师:这里有3种不同的表示方法,第1种能看懂吗?怎么来的?
生:直接数。
师:第2种呢?
生2:用每行的小正方形的个数乘行数。
师:说得真好!在大正方形里,由于每行的小正方形的个数等于行数。因此,我们可以用每行小正方形个数的平方即可算出。
师:按这种规律,那第5个图形的小正方形个数为?第n个图形呢?
生:52,n2。(板书5的平方)
师:这就是第2种方法体现出来的规律。
师:第3种有点特殊,谁来给我们讲一讲?(上台边指边讲)
生3:“1”是指第一个图形有1个小正方形;“1+3”表示在第一个图形的基础上增加了3个小正方形;“1+3+5”表示在第二个图形的基础上增加了5个小正方形……
师:感谢这位同学,他提醒我们可以这样一层一层地观察(撕下白纸层)。按照这种思路,同学们,第1个图形有几层,第2个图形呢?(2层,3层……)
师:继续下去,第5个图形有几层,以及对应的加法算式是什么?
生:第5个图形有5层,加法算式是1+3+5+7+9+11.(板书)
师:同学们回答得都非常正确。第5个图形就是在4乘4的图形基础上再增加一层,变成边长为5的大正方形。(贴板书)
师:看来,每个大正方形都有与之对应的算式。同一个图形,观察角度不同,可以写出不同的表示方法。
师:既然这里的乘法和加法算式都表示小正方形的个数,那这两种表示方法有什么联系?(相等)它们呢?(也相等)
师:好,那我们就用等号把它们连接起来。
师:接下来,请同学们仔细观察这些算式,它们有什么特点?(先独立思考,小组成员之间相互讨论,3分钟)
师:时间到,哪个小组来汇报下你们的讨论结果。
生1:从1开始加起;
生2:都是奇数相加;
生3:这些奇数都是连续的;
生4:有几个数相加,就是几的平方。
师:同学们观察的非常细致,找到了这么多的特点。如果我们把这些规律归纳总结成一句话是什么呢?谁来试一试?
生:从1开始的几个连续奇数相加,和就是几的平方。
师:归纳总结的非常准确且完整,请坐。接下来,我们全班一起把这句话读一遍。
师:咦,原来这些图形中隐藏着数的规律,我们可以用算式表示出来,这就是形中有数。反过来,是不是给你一个算式也有一个形等着它呢?
(二)体会数中有形
师:观察下面数的特点,它的结果是多少?你能想象一下,这个算式对应哪个图形吗?
出示题目:1+3+5+7+9+11 = ?
生:这个算式的结果是36,对应的是边长为6的正方形,有6个数相加。
……
师:(课件显示边长为6的大正方形)很好,同学们都能迅速地在脑海里想象出图形的样子。
师追问:刚才有学生说是边长为6的正方形,这个6可以怎么快速得到?
生1:因为1加到12共有12个数,12个数中有一半偶数,一半奇数,所以应该有12的一半,即6个奇数,因此是6的平方。
生2:6表示每行小正方形的个数,要求每行小正方形的个数,我们要看最后一层,这里最后一层有11个,而每行个数与行数相等,且重叠了1个小正方形,因此,我们可以用(11+1)除以2=6算出。
师:大家听懂了吗?好,我们用这种方法试试这个题。
出示题目:1+3+5+7+9+11+13+15 =
师:算式的结果是多少?对应哪个图形呢?
生:齐答(结果是82,对应的是8乘8的正方形。)
师:接下来,你能自己写出一个类似的算式吗?先完成任务三,然后同桌相互交流一下。(1分钟)
师:你觉得他们写得怎么样?谁能给我们解释解释?
教师通过手机拍照,展示学生成果。同时点学生进行评价。
(三)介绍正方形数
师:原来,像这样的算式都有一个正方形与它对应,这就是数中有形。以后再遇到特殊的算式求和,我们可以借助图形进行分析思考,这便是数形结合的优越性。
师:在这里,我们得到的小正方形数1,4,9,16……在数学中,我们把它称为平方数或正方形数。除此之外,到了中学我们还会继续研究三角形数、五边形数等等。
三、巩固练习,加深理解
师:通过刚才的探究,让我们感受到形中有数,数中有形,数形结合的好。接下来,我们利用所学的方法去解决其他的数与形问题。
(一)基础练习
1.请你根据例1的结论算一算。
(1)1+3+5+7+9+11+13+15=( )
(2)________________________=9的平方
(3)1+3+5+7+9+11+13+11+9+7+5+3+1=( )
(4)1+3+5+……+49=( )
师:请同学们在作业单上完成。
师:谁来说一说,你是怎么做的?
生1:第1题我是直接根据规律算出结果。
生2:第2题我是逆向运用规律写的。
生2:第3题,我把这个算式看成两部分,第一部分是7的平方,第二部分是6的平方。
生3:第4题,我用(1+49)除以2得到25个数,所以是25的平方。
师:看来,只要我们抓住算式特点,根据规律就能直接算出结果。
(二)综合练习
师:接下来,请同学们独立完成第2题。
2.下面每个图中最外圈各有多少个小正方形。
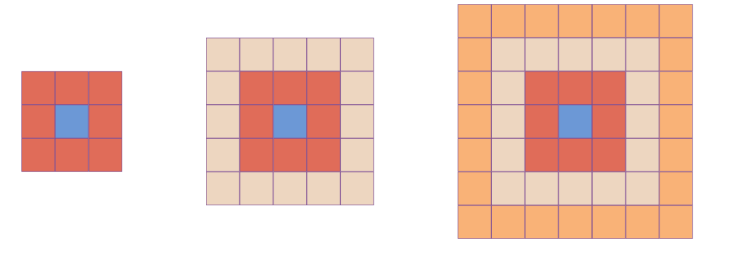
照这样画下去,第5个图形最外圈有多少个小正方形?你能解释其中的道理吗?
师:有没有同学愿意分享下你的思路?
生1:从计算结果看,最外圈的小正方形个数就是n的8倍,第5个图形最外圈有40个小正方形。
生2:我还可以根据规律往后继续写两个算式,从而计算出第5个图形最外圈小正方形的个数。
师:其实老师还发现了一个规律,请看,52-32=(5-3)(5+3)……为什么会这样呢?这是一个重要的计算公式,老师在这里先卖个关子,等同学们进入初中后就会研究这个问题。
(三)拓展练习
3.选一选。
2+4+6+8+10+12=( )
A.6的平方
B.6的平方+6
C.7的平方
想一想:上面这个算式对应了那个图形?
师:谁来说说你是怎么做的?
师:接着,想一想,这个算式对应那个图形呢?
生:6乘7的长方形。
师:你的空间想象真棒,还有其他同学也想到了吗?
师:我们一起来看看吧。
师:那算式中的这些数在那里?
生:在这里(边指边说)
师:哦,原来这些数是在这藏着的。
四、课堂小结,课后延伸
师:同学们,通过今天的学习,你有哪些收获呢?
生1:我知道了,从1开始的几个连续奇数相加,和就是几的平方。
生2:形中有数,数中有形,数形结合可以帮助我们解决问题。
师:很好,只要把数和形紧密的结合起来,解决问题会变得更简单,数学也会变得更加有趣。
师:今天的课就上到这里,同学们下课。