毕达哥拉斯说：数统治着宇宙。伯克霍夫说：“整数的简单构成，一直是使数学获得新生的源泉。”在整个数学中，数论（对数的研究）分支是最“美”的，像一座长满奇异花草的大花园。而对一些特殊数的探究，吸引着众多的专家和数学爱好者用大量的精力去研究而乐此不疲。

下面介绍几种特殊的自然数。

1.完全数

如果一个自然数等于除它自身以外的各个正因子之和，则这个数叫做完全数。完全数是被古人视为瑞祥的数，古希腊人在公元2世纪末已发现了四个完全数。最小的一个完全数是6=1+2+3。意大利人把6看成是属于爱神维纳斯的数，以象征美满的婚姻。

在自然数里，到底有多少完全数呢？有人作过统计，在1到40000000这么多数里，只有5个完全数，它们是

6=1+2+3

28=1+2+4+7+14

496=1+2+4+8+16+31+62+124+248

8128=1+2+4+8+16+32+64+127+254+508+1016+2032+4064

还有一个完全数是3350336。可见完全数是非常稀少的。

从第四个完全数8128到第五个完全数33550336的发现经过了一千多年，这是因为第五个完全数要比第四个完全数大了4100多倍。这可能是历经一千多年才艰难跨出一步的原因。

完全数还有一些鲜为人知的性质，如：

（1） 所有完全数都可以表达为2的一些连续整数次幂之和，如图1，

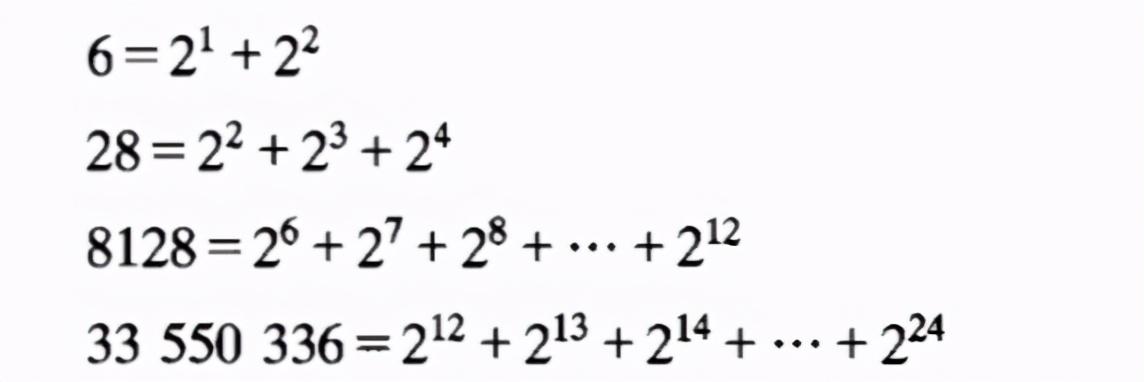
图1

（2） 除了6以外，其他完全数可表示为连续奇数的三次方之和，如图2

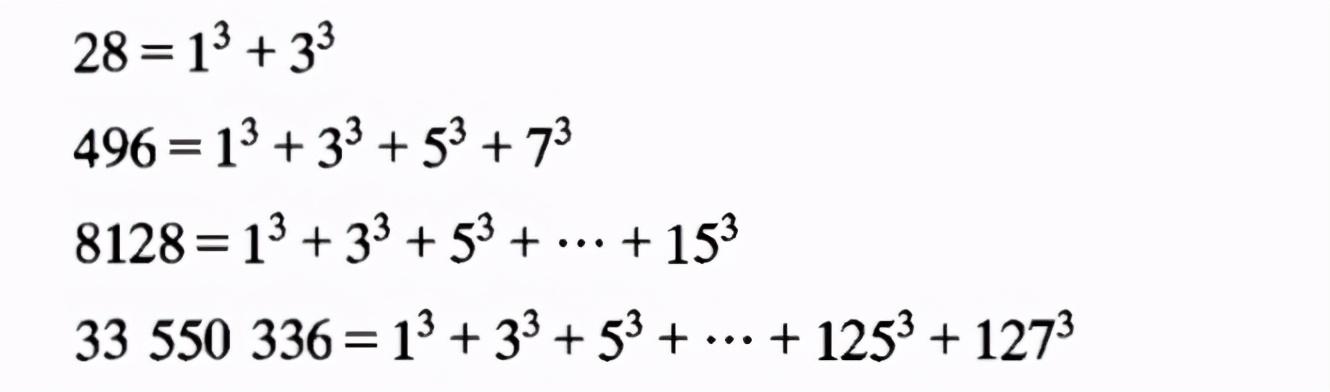
图2

如此完美的模式，难怪完全数如此的迷人，具有魅力，因此，完全数是极美的数。

（3）迄今为止，发现的完全数都是偶数，还没有发现一个奇完全数，但也没有证明奇完全数不存在。

（4）迄今为止，发现的完全数都具有以下的形式N=2^(n-1)( 2^n-1）（其中n与2^n-1都是素数）

2.亲和数

若自然数M的全部正因子（去掉其本身）之和，恰为自然数N，而N的全部正因子（去掉其本身）之和恰为自然数M，则称M、N为一对亲和数。最简单的一对亲和数是220和284，把220的全部正约数（不包括220本身）加起来为

1+2+4+5+10+11+20+22+44+55+110=284；

而把284的全部正约数（不包括284本身）加起来为1+2+4+71+142=220

想不到枯燥的数字之间也有这种“我中有您，您中有我”的亲密无间的“相亲数”。在毕达哥拉斯时代就知道有这一对亲和数。当时人们认为只有这一对亲和数，一直延续了两千多气年，人们对此坚信不移。直到1636年皮勒发现并公布了第二对亲和数17296和18416，这才破除了只有一对亲和数的迷信，也激发起了寻找更多亲和数的热情。

如今，人们已经发现了1200对亲和数。电子计算机出现后，人们可以用高速度大容量的计算去探索更多的亲和数。人们现在已知最大的一对亲和数是111 448 537 712和118 853 793 424，要把它们的因数找出来再求和，推证它们之间的关系，没有现代计算机工具的帮助是很困难的。

3.完全平方数

一个整数的平方称为完全平方数，简称平方数。如：1、4、9、16、25、36、49、64、81、…… 都是平方数。在整数中除了素数外，最引人注目的就是平方数。平方数在正整数中比素数更加稀疏，且具有规律性。不超过正整数n的平方数（不算0）的个数是根号n的整数部分。

在哪些情况下可以出现完全平方数？

（1）前n个奇数的和一定是平方数。

（2）前n个正整数的和有可能是平方数，如1+2+3+…+8=6^2,1+2+3+…+49=35^2，……这种和数中包含的平方数有无穷多个。

（3） 四个相邻正整数的乘积与1的和一定是完全平方数，

例如1·2·3·4+1=52,2·3·4·5+1=112,3·4·5·6+1=182,5·6·7·8+1=292。

一般地有，如图3所示

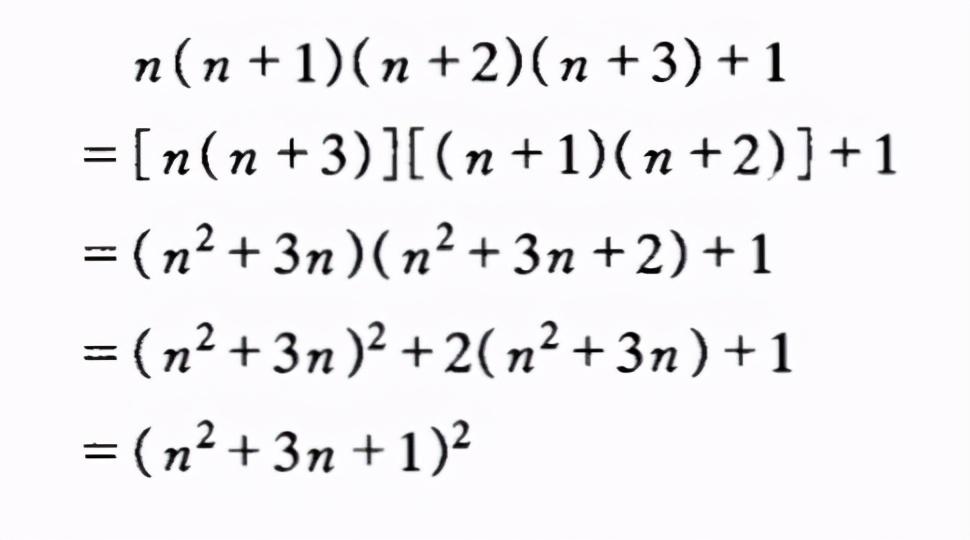
图3

4.多边形数

多边形数是这样的数，它的形状与多边形的形状有着密切的关系，例如（图4~图6）：

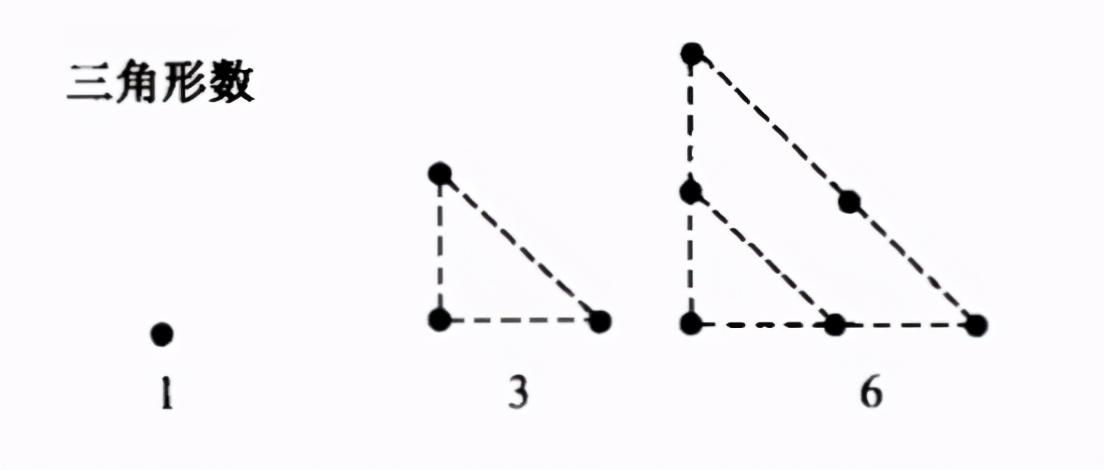
图4

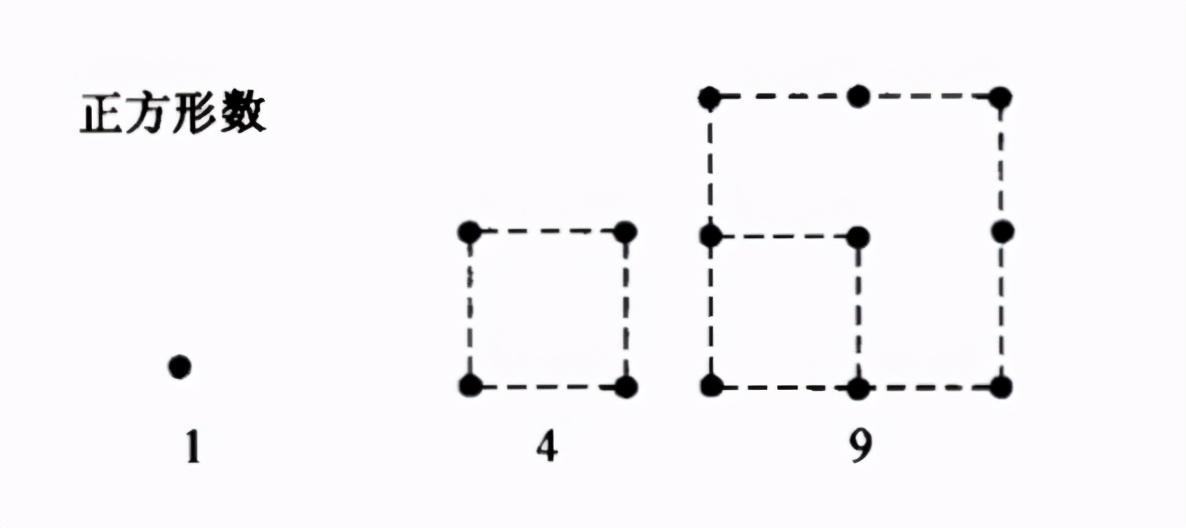
图5

图6

5.勾股弦数

我们把满足不定方程a^2+b^2=c^2的正整数a、b、c称为勾股弦数。

我国古代数学书《周髀算经》中，就已有“勾三、股四、弦五”的提法，即3^2+4^2=5^2。

在刘徽的《九章算术注》中，又记录了5^2+12^2=13^2，

8^2+15^2=17^2,7^2+24^2=25^2,20^2+21^2=29^2，……许多组整数解。

古希腊数学家毕达哥拉斯指出，当n是奇数时，n, (n^2-1)/2，(n^2+1)/2是勾股弦数。

现在大家都知道，勾股弦数是无穷无尽的，而且许多的勾股弦数都能由下面的公式（见图7）

图7

勾股弦数正好满足直角三角形三边关系，即勾股定理。

是否有满足a^2+b^2+c^2=d^2的正整数解a、b、c、d呢？

回答是肯定的。同时想要举出这样的数组并不困难。只需将两个勾股数相加，便可得到，如3^2+4^2=5^2和5^2+12^2=13^2相加即得3^2+4^2+12^2=13^2，又如8^2+15^2=17^2和9^2+12^2=15^2相加即得8^2+9^2+12^2=17^2。

6.还有许多有趣的数

（1）魔术数：如果一个数接写在另一个数后面，所得到的新数能被这个数整除，则这个数称为魔术数。如2接写在37后面得到372，能被数2整除，数2是一个魔术数。

（2）缺8数：如今人们把“8”与“发”划上等号，指对它的青睐。然而，有许多人竟在研究一个缺8数12345679。这个数有许多有趣的性质：例如（见图8）

图8

缺8数还有许多有趣的性质等待人们去发掘。

（3）史密斯数：美国数学家阿尔伯特·威兰斯基在同他姐夫史密斯交谈时，发现他的电话号码4937775是几个素数的积3×5×5×65837表示的合数。这些数之和3+5+5+6+5+8+3+7=42，而这个数各位数字之和4+9+3+7+7+7+5=42也是42.我们称具有这种性质的数为史密斯数。

图9

在奇妙的数的世界里遨游，不但能开阔眼界，还能启迪人的智慧。