《易·系辞》中说：“上古结绳而治，后世圣人易之以书契”，说明古人结绳和契刻的方式记数和记事。西安半坡村出土的陶器上有直线、三角、方、菱形及一些复杂的几何图形，同时期人们创造了画圆和画方的工具规和工具矩，中国的数学可以追溯到5000到6000年前。

半坡陶符光影图

然而，很多人认为中国的古代数学其实不是数学，最多被称为算术或者算学，不同于西方以古希腊为代表的基于逻辑推理下的数学。比如：勾股定理，无论是有记载或者没记载的，虽然中国对其发现早于西方几百年，但长时间的知其然，不知其所以然。我们对其证明要晚于西方数学界，直到现在西方数学也称该定理为“毕达哥拉斯定理”，毕竟人家是有记录的第一个把勾股定理给予证明的！

事实上，中国的数学并不是不堪一击，我们今天讲的球的体积公式，确实是由中国人一板一眼的推出来的！并且推导过程均是胜在取巧，本文将出现的三个关键词：《九章算术》，刘徽，祖暅！让我们一起来领略古代数学的魅力！

一、《九章算术》

《九章算术》，作者不详，经西汉的张苍、耿寿昌等人删补而成，在唐宋两代，它是朝廷明令要求的官方数学教科书，也就是说虽然高考不考，但是也算是必修课程。

《九章算术》的“少广”章主要解决两个问题，“开方术”和“开立方术”，该章的第二十四问：“又有积一万六千四百四十八亿六千六百四十三万七千五百尺。问为立圆径几何？”也就是问：“已知体积是1644866437500尺的球，求这个球的直径是多少？”

具体方法在“开立圆术”这样说道：“置积尺数，以十六乘之，九而一，所得开立方除之，即丸径。”意思是说：“把体积乘以16，再除以9，然后开立方，就得到球的直径了。”

更直白的说，《九章》认为正方体的体积和它的内切球的体积之比是：16：9。用现代数学的观点来看，显然不精确，但是在当时已经是非常了不得了。那么，这个16:9是如何来的呢？这里要引入古代数学中常见的两个名词：“方”和“圆”，一个正方形和一个圆形。现在我们知道正方形和它的内切圆的面积之比是4：π，由于古代《周髀算经》对圆周率有“径一周三”的记载，故圆周率取3，就得到了“方”和“圆”的面积之比是4:3。

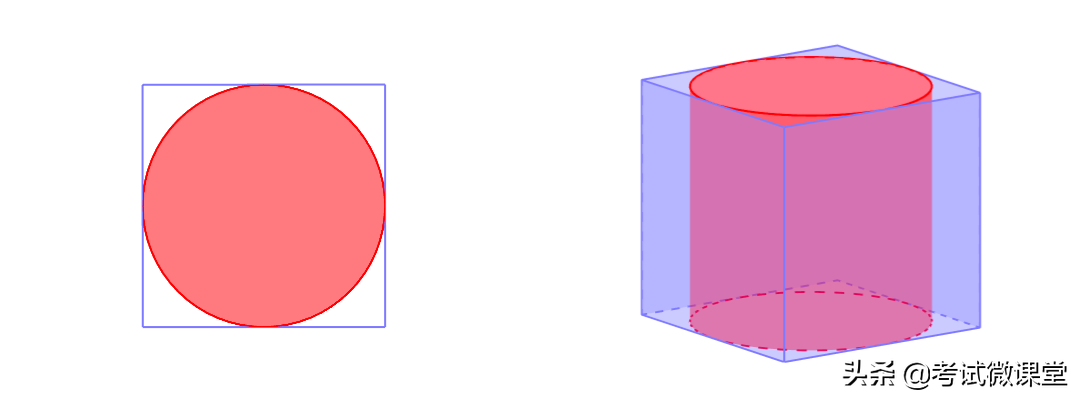
最后，把圆柱体视为“方”，把球体视为“圆”，由于“方”：“圆”=4:3，所以得到这个两个公式：正方体：圆柱=4:3；圆柱：球=4:3。所以正方体：球=16:9。

虽然不是很精确，但也不得不佩服古人的智慧，古人用圆柱作为过渡量，而不是粗暴的将“方”“圆”做比例。

二、刘徽

刘徽，魏晋时期伟大数学家。著有《九章算术注》和《海岛算经》。

就在他为《九章》做注的时候，发现上述推理过程中的错误，即“圆柱：球=4:3”是错误的。我们可以把原公式中的3还原成π，那么得到“圆柱：球=4:π”。现在不妨用现在数学知识进行推导，设球半径是r，圆柱的高是2r，则圆柱体积=2πr³，而球体积=4/3πr³，二者之比=3:2。确实是问题比较大。

发现问题，就要解决问题。如何能正确得到球的体积公式呢？正所谓“从哪里跌倒，就从哪里爬起来”，我们的刘徽还是从正方体出发。他构思了一个看似奇葩，却有确实有效的物体，它叫做“牟合方盖”。

这里的“牟”意思是相同。“盖”意思是伞。“牟合方盖”就是指两个面合在一起的两个相同的方伞。它是由一个正方体出发，先用竖直方向的内切圆柱截正方体，得到一个圆柱体，再用水平方向的圆柱再截一次，两个圆柱的共同部分所形成的几何体，就叫做“牟合方盖”。

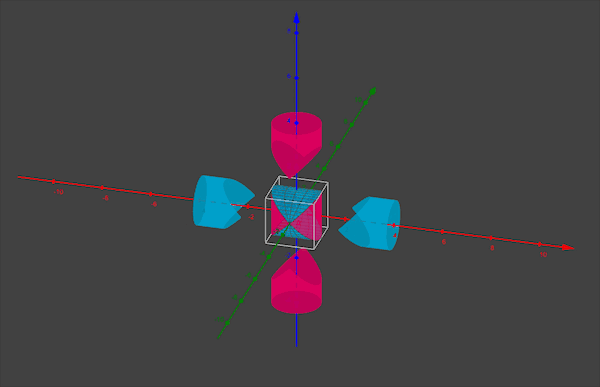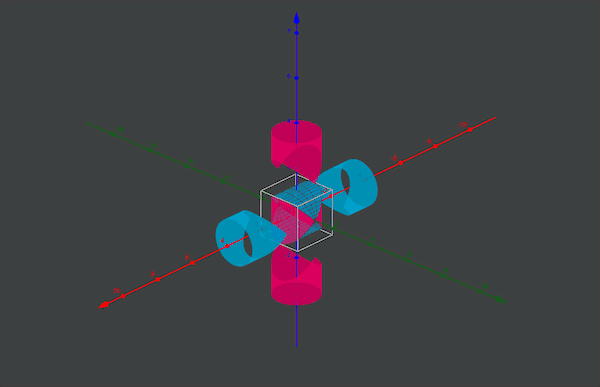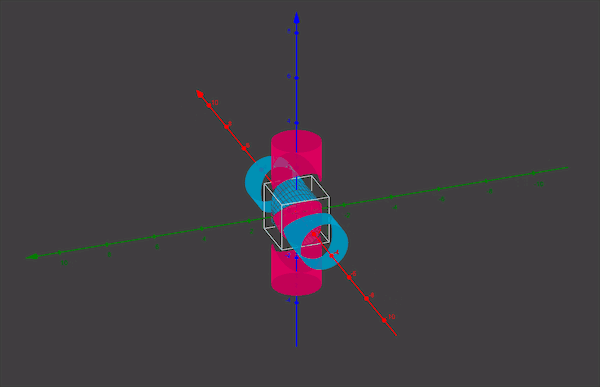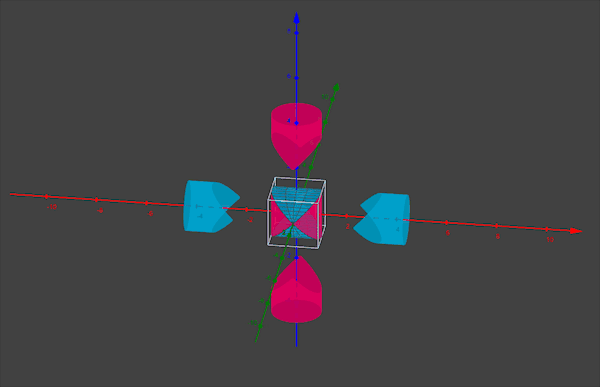
看似容易的一个方盖，这一创举足以让刘徽名垂青史，虽然刘徽的贡献还有很多，比如我们都知道圆周率和祖冲之，但殊不知祖冲之计算圆周率的理论支撑是“割圆术”，而“割圆术”的发明者正是刘徽，并且刘徽将圆周率计算到3.14，只不过祖冲之的圆周率更精确罢了。牛顿说：“我之所以比别人看得远一些，是因为我站在巨人的肩膀上”，此时祖冲之有话说：“巨人肩膀，我们都值得拥有！”

“牟合方盖”恰好把正方体的内切求包含在内，并且二者是相切的关系。如果用一个水平面去截方盖，会得到一个正方形和一个内切圆，二者的面积比例是4：π。从而得到“方盖”和“球”的体积之比是4：π。现在所有的工作重心落在了如何求出“牟合方盖”的体积，一旦求出该体积，球的体积瞬间即可攻破！

此时，剧情出现了转折，刘徽说：“敢不阙言，以侯能言者。”翻译过来就是：“我弄不了了，谁行谁上吧！”显然，就当时的社会情况，你刘徽大神都搞不定，谁能接住这个活啊？至此，球的体积告一段落。让我们一起等待另一个巨匠的出现！

三、祖暅

祖暅[gèng]，南北朝时期，祖冲之之子。不得不佩服祖氏一家这优秀的基因，打虎亲兄弟，上阵父子兵，爷俩互相学习，共同发展，也是当今社会亲子关系的典范！

祖暅认为，要想成就一番事业，巨人的肩膀还是要踩的，自己的爸比用了刘徽的“割圆术”，成功的精确的计算了圆周率，荣登数学大神之列，而他将用刘徽大神的“牟合方盖”，继续为祖氏家族添光加彩。

小祖同学知道球的体积就是卡在如何求出“牟合方盖”体积，而他选择攻破的恰恰就是这个方盖的体积。显然硬算肯定是不灵的，必须要取巧。

也许在某一年的某一天，祖暅在家里闲着无事，看着一些铜钱发呆。他发现：这两摞铜钱，每摞十个，无论怎么样摆放，这两摞铜钱的体积一定是相等的。这么弱智的结论激起了祖暅的好奇心，为什么会这样呢？

原因是它们在任意截面处有相同的面积，所以它们的体积是相等的。在此基础上，诞生了著名的“祖暅原理”：幂势既同，则积不容。就是说：如果两个几何体在任意截面处的面积都相等，那么这两个几何体的体积是相等的！要知道在西方，需要等到一千年后，由意大利数学家卡瓦列利才提出这一原理。

有了这个原理，就不需要硬求“牟合方盖”的体积了，只需要找到一个和“牟合方盖”体积相同的几何体，这个几何体需要满足两个条件：①简单易求，②与方盖满足“幂势既同，则积不容”。

又到了脑洞大开的时间，这个几何体终于被小祖同学找到了。

首先，小祖把“牟合方盖”进行8等分

我们把它称之为8个“小方盖”，切割方法是：俯视方盖，横竖两刀，正视方盖，横着来一刀。（如果想象不出来，不妨做一道小学奥数题：如何用三刀把一块蛋糕分成八块？）这个时候只一个小方盖，整个方盖就搞定了。

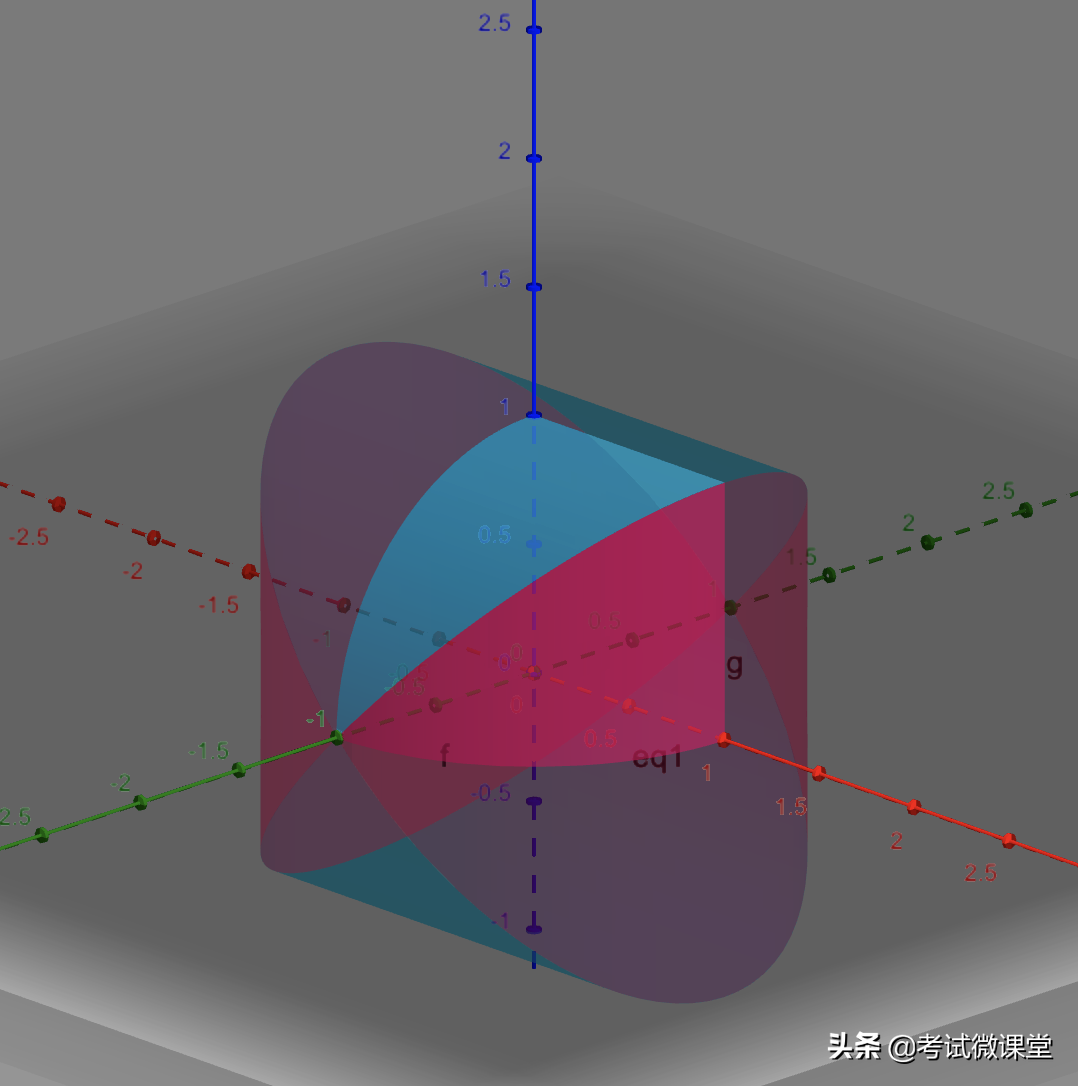
牟合方盖被8等分

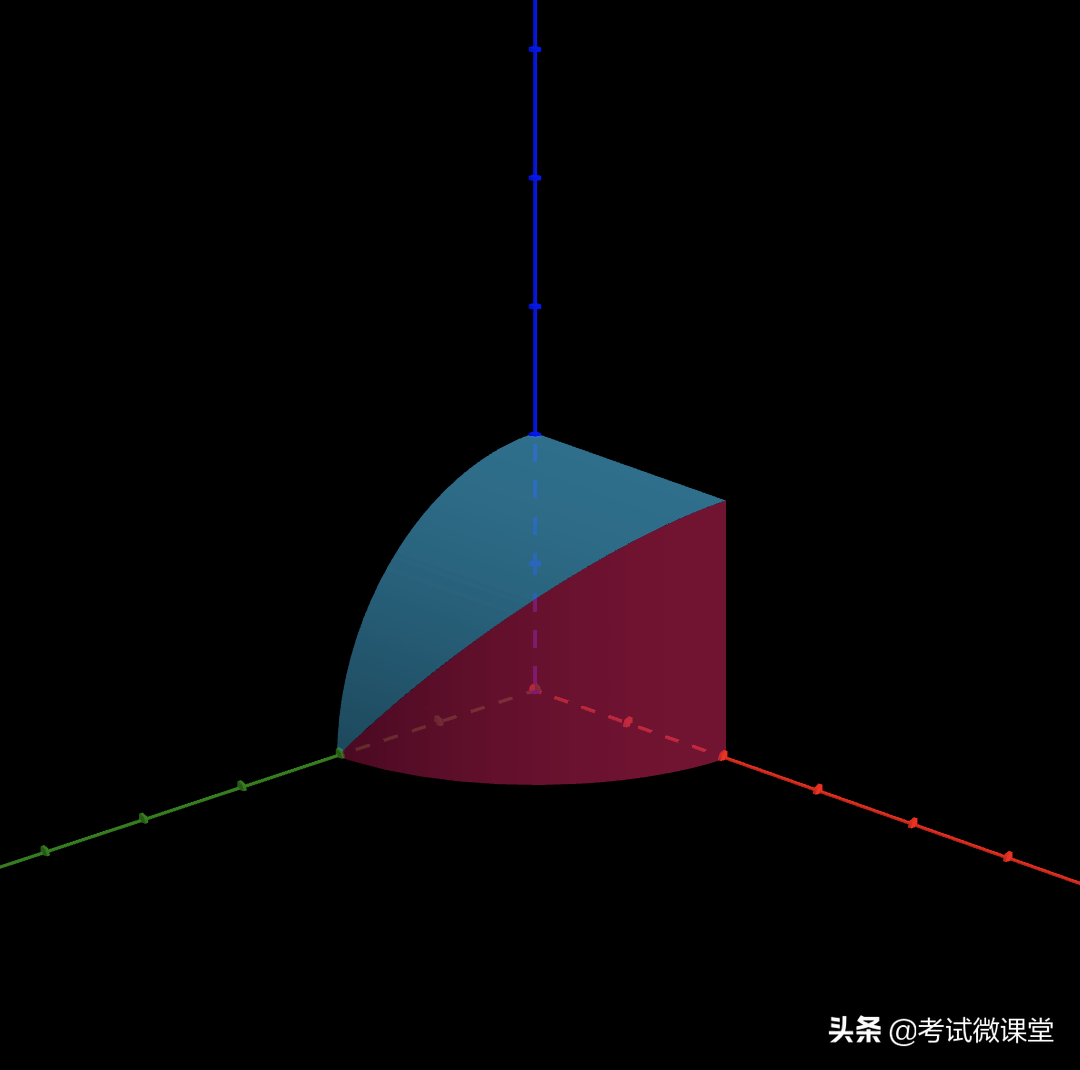
牟合方盖被8等分后，其中的一块

接下来，小祖发现，找到这样的一个几何体还是很困难的，再次“取巧”，动用“割补法”

当我们求不出目标几何体的体积，试图把它不成一个规则的几何体，再减去剩余部分就行了。接下来我们详细展示一下小祖是如何运用“祖暅原理”求出“小方盖”的体积的。我们会用到大量的现代数学符号，而当时小祖同学却没有这些便利的工具，所以说小祖同学的智力确实是卓越非凡的！

设球的体积是r，将“小方盖”放在棱长为r的正方体中，定义：把正方体中除去小方盖部分称为“小方盖剩余”，找到与其“幂势既同”的几何体。先计算图二的阴影，在用正方形的面积减图二阴影，得到图一的阴影面积。再构建一个倒放的四棱锥，使得与“小方盖剩余”符合“祖暅原理”。

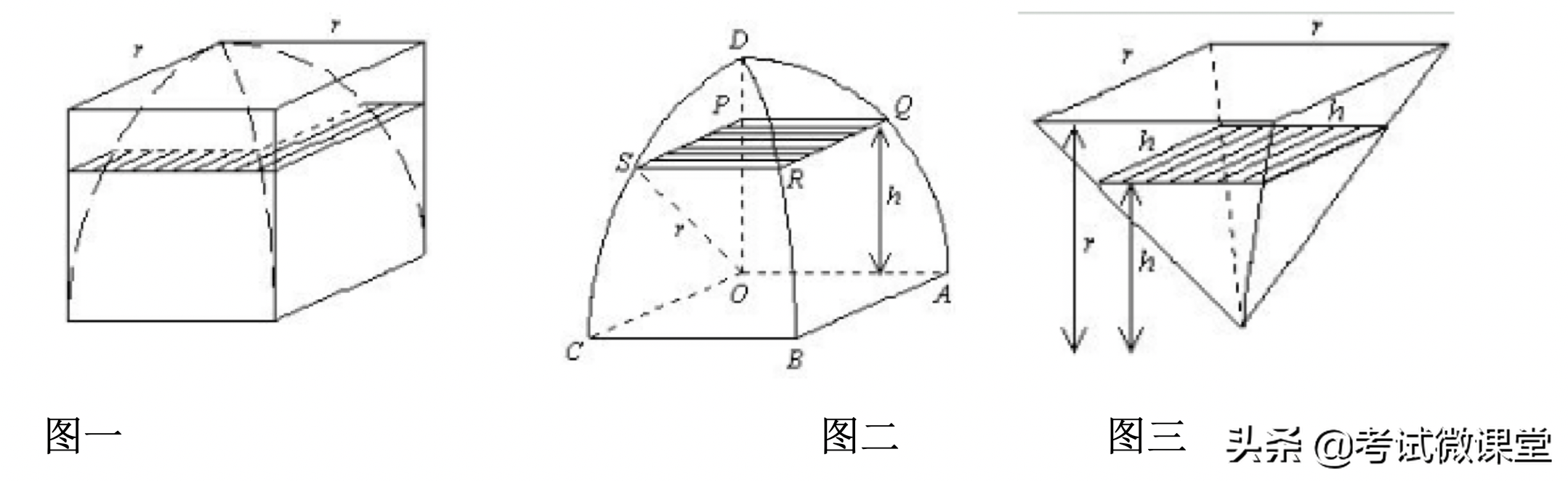
具体过程：

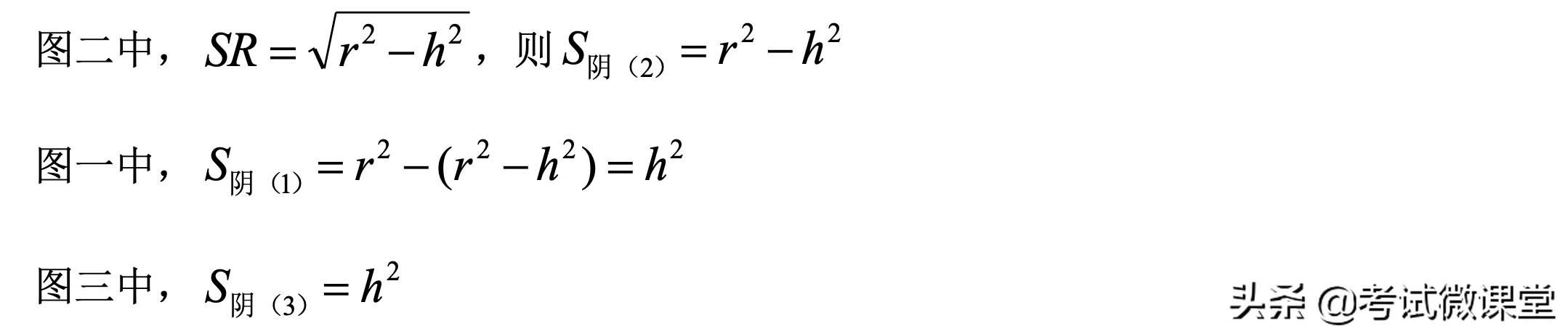
这样来看图三的四棱锥的体积与小方盖剩余的体积必然相等。则：

再根据刘徽的体积比例：“方盖”和“球”的体积之比是4：π，此时可得到球的体积是4/3πr³，这就是世界公认的球体积公式。球的体积公式是由中国人独立研发，先后经历三个版本，经过千年测试均可完美运行。更重要的，其推理方法，附属定理，让解决其他数学问题变得有章可循！

经过几代人的努力，终于使中国数学在世界范围内留下了光辉灿烂的一笔！

确实，中国古代数学不同于古希腊数学，是完全的另一套体系，我们的内容多来自生产与实践，算法程序化和机械化，注重应用。在算法上，我们说第二，就无人敢说第一！比如，十进位制、今有术、盈不足术等等算法，曾经传到印度和阿拉伯，再由这些国家传到欧洲乃至全世界，对世界数学的发展起到非常大的促进作用！