旋转矩阵的推导过程
如下如图所示,两个坐标系X-Y-Z及X1-Y1-Z1,它们的原点及Z轴重合,X1-Y1-Z1绕Z或Z1轴旋转了角度φ。有一个点p,其在X-Y-Z坐标系下的坐标为(x,y,z),且假设其在X-Y-Z中固定不动。在X1-Y1-Z1坐标系下的坐标为(x1,y1,z1)。注意:此时Z、Z1轴垂直于纸面向外。坐标(x,y,z)与(x1,y1,z1)之间存在着怎样的运算关系呢?注意:φ的正负按右手螺旋定则来判定,拇指指向旋转轴的正向,此时若旋转角度的方向与食指中指指向一致,则角度为正,若方向相反则角度为负,以下推导不在赘述。
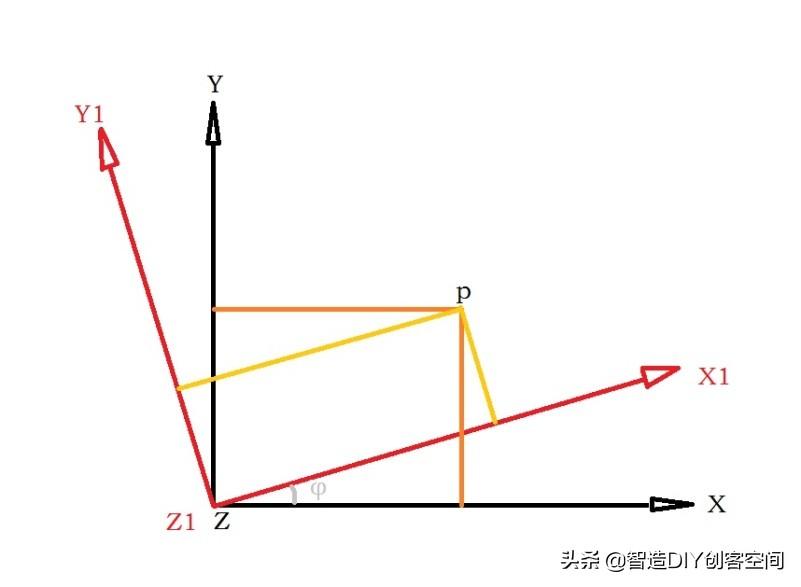
从图中的几何关系,将(x,y,z)看作已知量,可以得到:

将以上等式关系写成矩阵的形式:
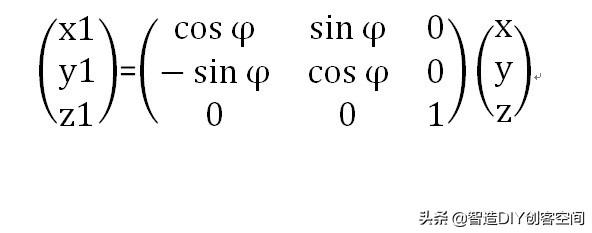
上式等号右边的第一个矩阵就是一个旋转矩阵,是绕Z轴旋转的旋转矩阵,注意这个矩阵是"左乘"向量(x,y,z),不能随意写成"右乘",如果要变换位置,必须把旋转矩阵和列向量(x,y,z)进行"转置",即把"列"换到"行"。上式是从(x,y,z)到(x1,y1,z1)的变换运算。
接下来,我从上图中Y轴的负方向往正方向看去,并且隐藏X-Y-Z坐标系,再建立一个新的坐标系:X2-Y2-Z2,其原点位置仍与X1-Y1-Z1重合,且Y1轴与Y2轴重合,X2-Y2-Z2坐标系绕Y1或Y2旋转一个角度θ。注意:此时两坐标系的Y轴是垂直纸面向里的,根据右手螺旋定则判定,此时θ应该是负的。
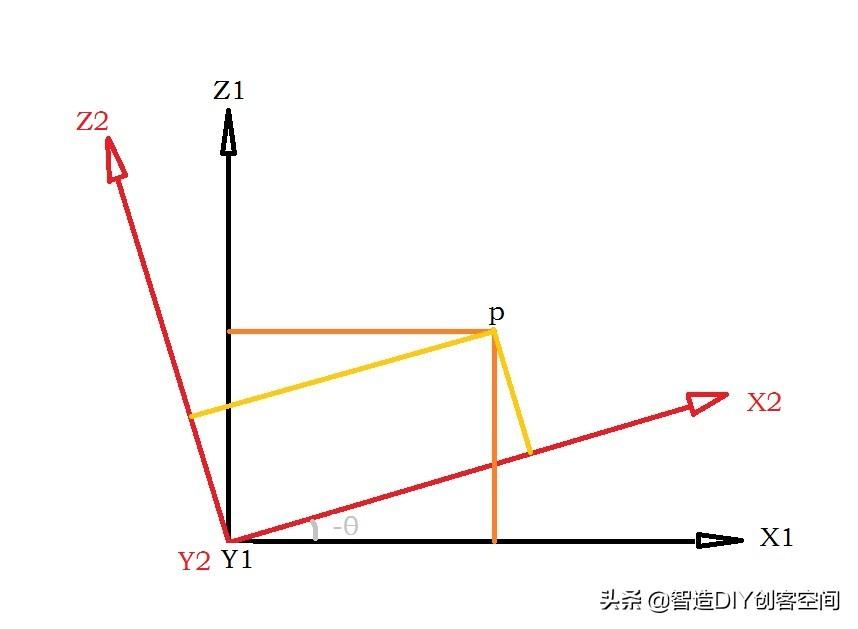
与前面的方法一样,我们可以很快得到下面等式:
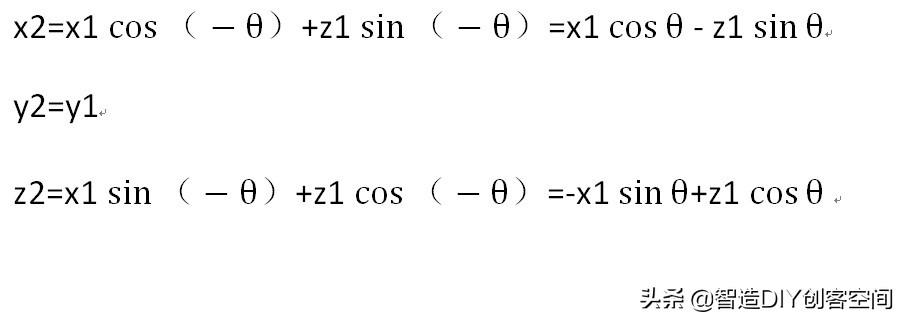
写成矩阵的形式得:
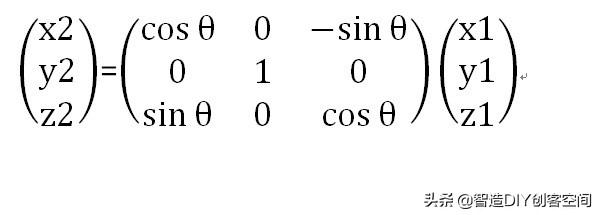
这个变换是从X1-Y1-Z1到X2-Y2-Y2的变换。
接下来,我们再从上图的右侧,即X1、X2的正向往负向看过去,隐藏X1-Y1-Z1坐标系,再次新建一个坐标系X3-Y3-Z3,它的原点仍然与X1-Y1-Z1重合,且X3轴与X2轴重合,X3-Y3-Z3绕X3或X2轴旋转了一个角度β。此时X2、X3是垂直于纸面向外,根据右手螺旋定则判定β的值为正。
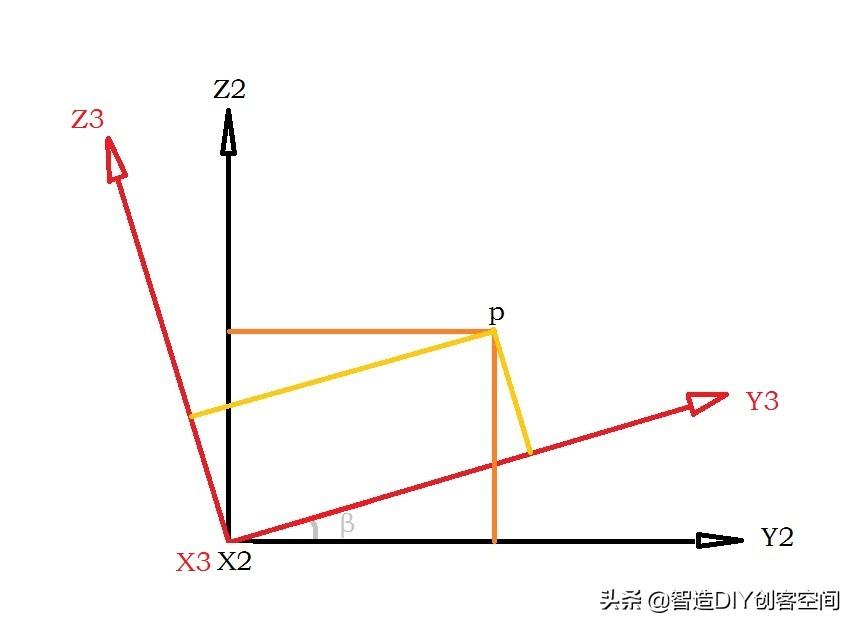
同样,我们可以很快得到下面等式:
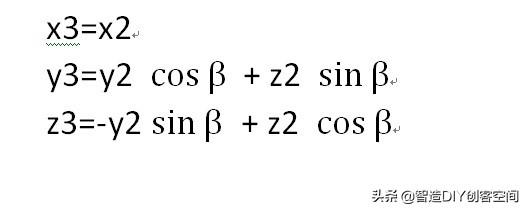
写成矩阵的形式:
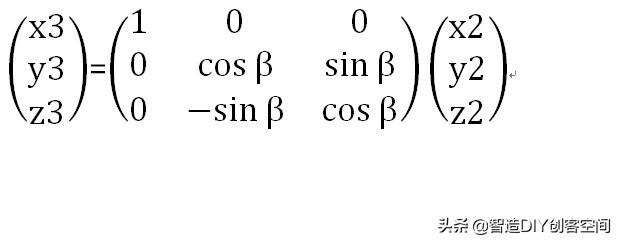
这个变换是从X2-Y2-Z2到X3-Y3-Y3的变换。
下面,我们隐藏X2-Y2-Z2,恢复X-Y-Z,此时的X3-Y3-Z3就是最开始与X-Y-Z重合的一个坐标系经过三次旋转得到的新坐标系,此时p点在X-Y-Z坐标系下的坐标仍为(x,y,z),而它在X3-Y3-Z3的坐标为(x3,y3,z3),则X-Y-Z坐标系到X3-Y3-Z3坐标系的变换为:
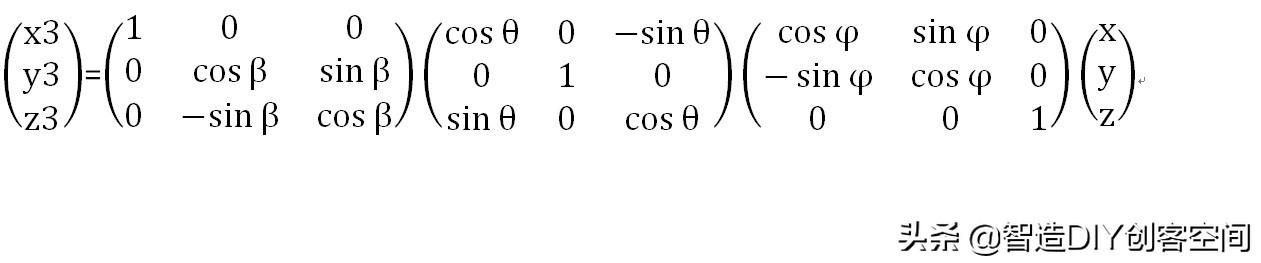
注意矩阵的"左乘"顺序,这个顺序是不能随意改动的,它必须与旋转顺序一致。实际上,我们是将(x2,y2,z2)、(x1,y1,z1)逐次代入得到上面等式的。旋转次序不同,得到的旋转矩阵是不一样的。在这个推导过程中,我们是先绕Z轴旋转,再绕Y轴旋转,最后绕X轴旋转。如果我们以一架飞机的坐标系来定义,X轴指向机头方向,Z轴指向飞机的上方,而Y轴指向飞机的侧面,绕Z轴旋转的角度称为偏航角-yaw(),绕Y轴旋转的角度就是俯仰角-pitch(θ),绕X轴旋转的角度则是滚转角-roll(β),因此本文中的旋转次序可以定义为y-p-r。接下来,按照矩阵乘法的规则(自左向右),整理上面的等式:
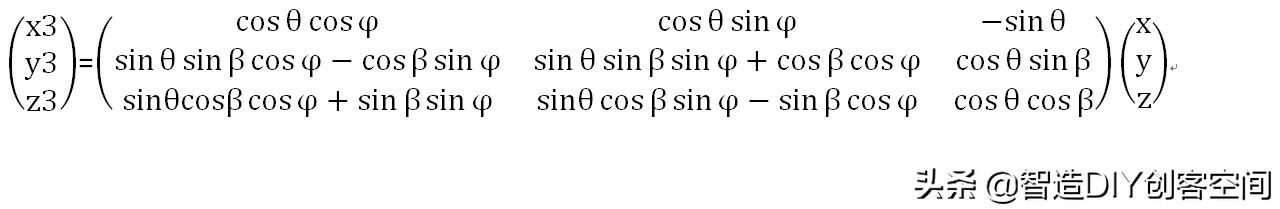
上面等式中,等号右边的3X3矩阵就是我们最终要求出的旋转矩阵。在整个变换过程中,X-Y-Z坐标系是固定不动的,例如地理坐标系,因此可以称为g系;而X3-Y3-Z3是相对于g系旋转的,可以把它理解为固定于一个飞机的机体(body)上,因此称为b系。通过上面得出的矩阵,我们可以把g系的坐标投影到b系,因此该矩阵也记为,表示从g-b的变换。如果要求b-g的变换,则要求出的逆矩阵。在线性代数中,求矩阵的逆矩阵是一个非常复杂的过程,然而非常幸运的是,是一个正交矩阵(这个定义将在后期文章中进行介绍),它的逆矩阵就是它的转置矩阵,因此,我们可以通过简单的"行列交换"得出其逆矩阵:
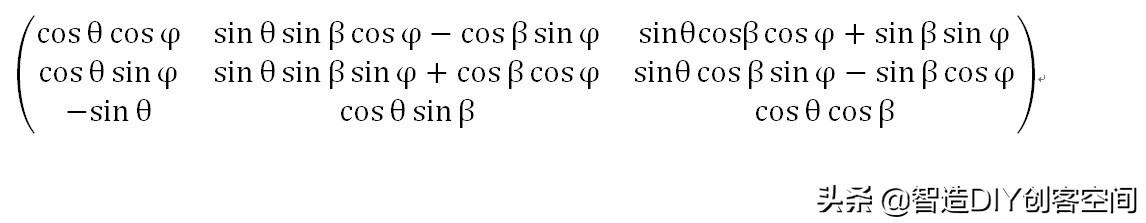
如果不嫌计算麻烦,我们也可以用"土"办法来验证,例如在绕Z轴旋转得出的等式关系中,将x1,y1,z1看作已知数,求解x,y,z关于x1,y1,z1的等式关系,三组等式都这样进行求逆,最后按上面的三个旋转次序再进行矩阵乘法,一定可以得到上面的矩阵。另外,通过旋转矩阵的元素,也可以求出当前b系相对于g系的欧拉姿态角。
在"旋转的四棱锥"项目中,g系就是固定在屏幕上的"屏幕坐标系",b系则是固定在四棱锥上跟随四棱锥旋转的"四棱锥坐标系",这个项目的核心就是这个旋转矩阵。
