※第一节需要掌握以下内容:
1、认识生活中的长方体和正方体
2、掌握长方体和正方体的棱、面、顶点个数,需要记住
3、认识长方体的长、宽、高
4、熟悉长方体和正方体的展开图,并可以通过各种展开图头脑里合成正方体或长方体。
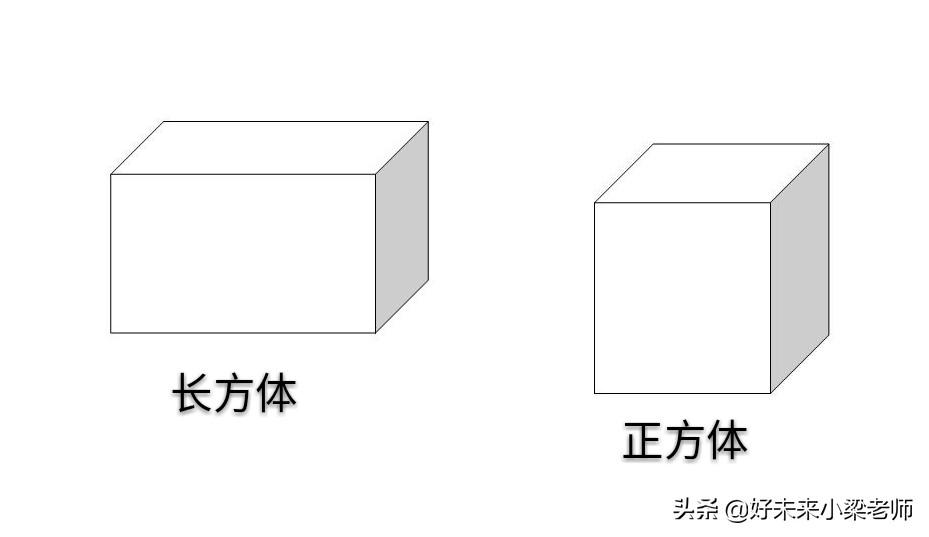
第一节知识点:
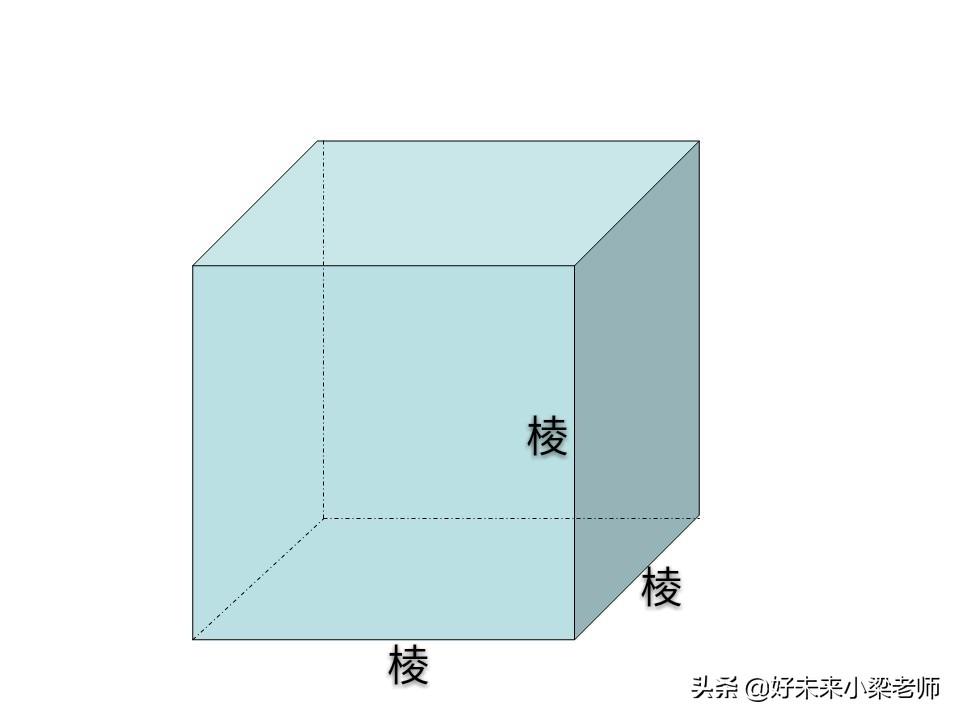
1、棱:两个面相交的线叫做棱。
顶点:三条棱相交的点叫做顶点。
2、长方体特征:
①长方体有6个面,12条棱,和8个顶点。
②长方体的面一般是长方形(也可能有两个相对的面是正方形),相对的面完全相同,相对的棱长度相等。
3、长方体相交于同一顶点的三条棱的长度,分别叫做它的长,宽,高。
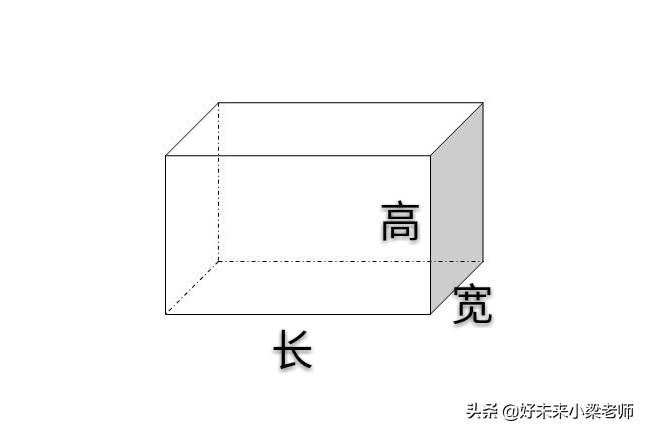
4、正方体特征:
①正方体和长方体一样,也有6个面,12条棱,和8个顶点。
②正方体的6个面是完全相同的正方形。所有的棱长度相等。
③正方体是特殊的长方体。
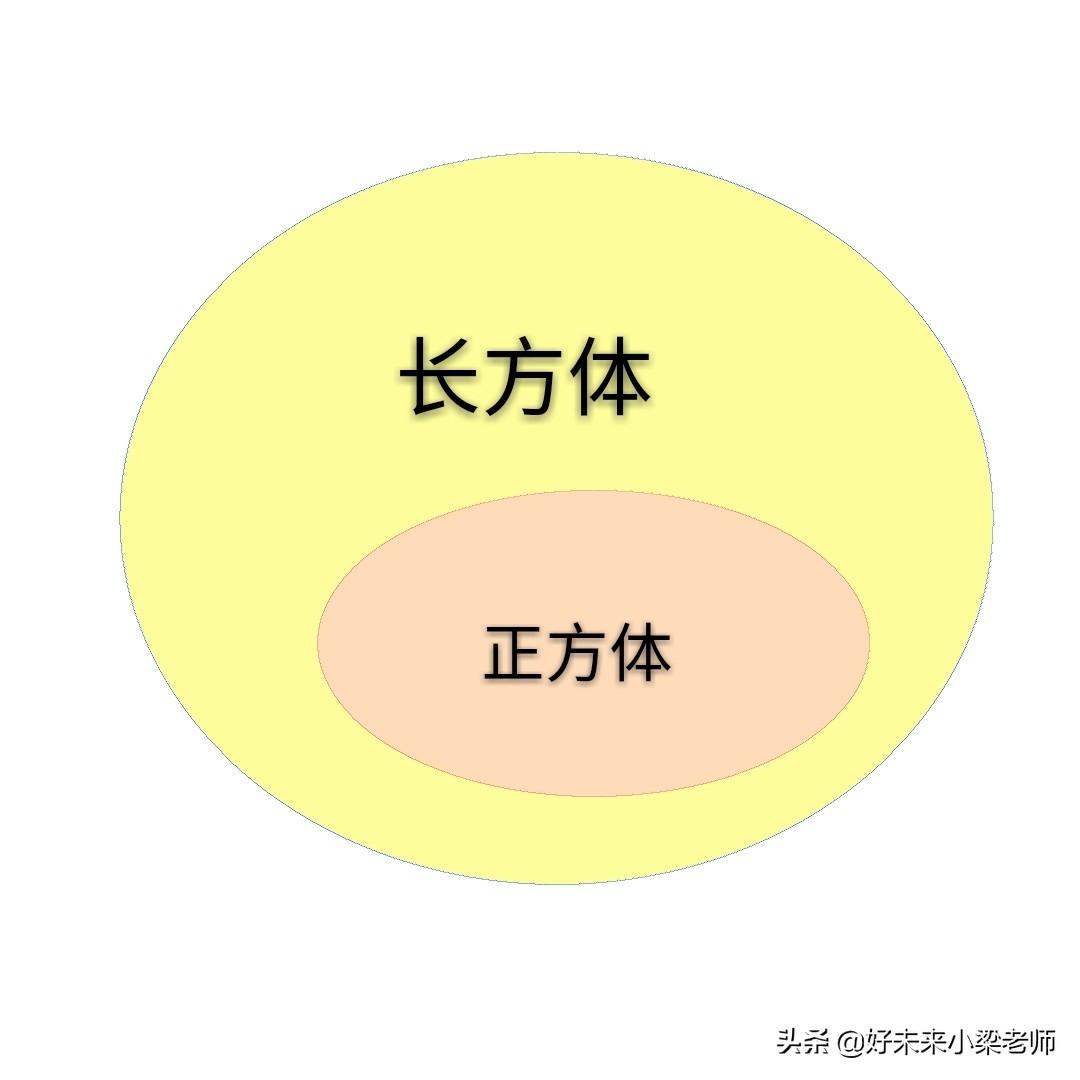
练习:课后“练习一”的题目预习完本节内容都可以做。
※第二节需要掌握以下内容:
1、计算长方体和正方体的表面积。
2、根据实际情况计算长方体和正方体的表面积。
第二节知识点:
1、长方体的表面积计算公式:
长方体表面积=(长×宽+长×高+宽×高)×2
这个公式不建议背,去理解的记忆。
这个公式表示,上下、左右、前后六个面的面积和。
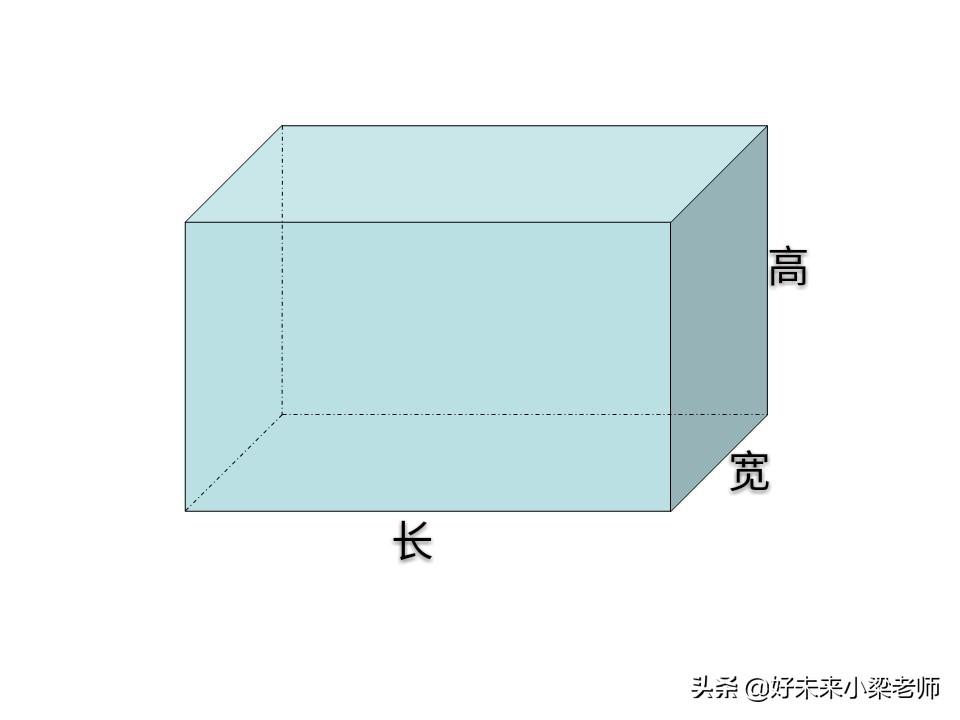
2、正方体的表面积公式:
正方体的表面积=棱长×棱长×6
3、用计算长方体或正方体表面积的办法解决实际问题时,要注意以下几点:
①根据实际情况确定计算哪几个面面积的和,实际情况有时候不需要计算所有面的面积。比如无盖的盒子的表面积。

②根据长方体面的特征,可以选择不同的方法计算。
练习:课后“练习二”的内容建议都做一下。
※第三节需要掌握以下内容:
1、什么是物体的体积?
2、什么是容器的容积?
3、体积单位有哪些?相邻单位的进制是多少?
4、容积单位有哪些?相邻单位的进制是多少?
5、根据给出的物体,估计物体体积的大小。
第三节知识点:
1、体积:物体所占空间的大小叫做物体的体积。
2、容积:容器所能容纳物体的体积叫做容器的容积。(简单来说,体积是指物体外部大小,而容积指物体内部大小)
3、常用体积单位有:立方厘米(cm³),立方分米(dm³),立方米(m³)。相邻两个体积单位进制是1000。
1立方米=1000立方分米
1立方分米=1000立方厘米
1m³=1000dm³
1dm³=1000cm³
①棱长1厘米的正方体,体积是1立方厘米。手指头的体积大约是1立方厘米。
②棱长1分米的正方体,体积是1立方分米。粉笔盒体积大约1立方分米。
③棱长是1米的正方体,体积是1立方米。
4、计量容积一般用体积单位。
如果是计量液体的体积,则用升或者毫升。
①1立方分米=1升(1dm³=1L)
1立方厘米=1mL(1cm³=1mL)
②容积是1立方分米的容器,正好盛水1升。容积是1立方厘米的容器,正好盛水1毫升。
练习:完成课后“练习三”所有内容。
※第四节需要掌握内容:
1、如何计算长方体和正方体体积的体积。
2、掌握长方体和正方体体积的计算公式。
3、进一步学习体积单位之间的换算。
第四节知识点:
1、长方体的体积公式:
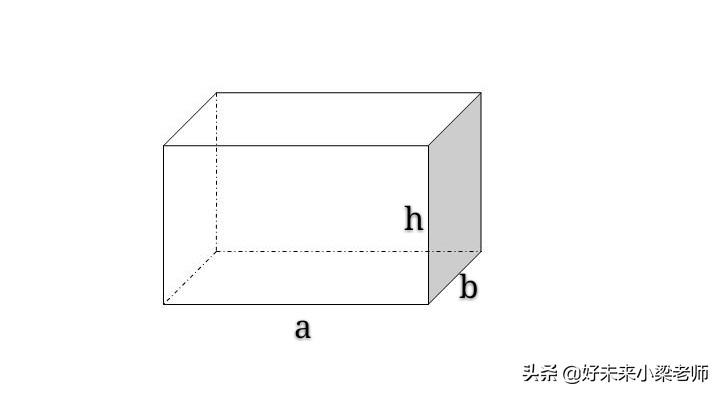
长方体的体积=长×宽×高
用字母表示:V=abh
(V表示体积,a表示长,b表示宽,h表示高)
2、正方体的体积公式:
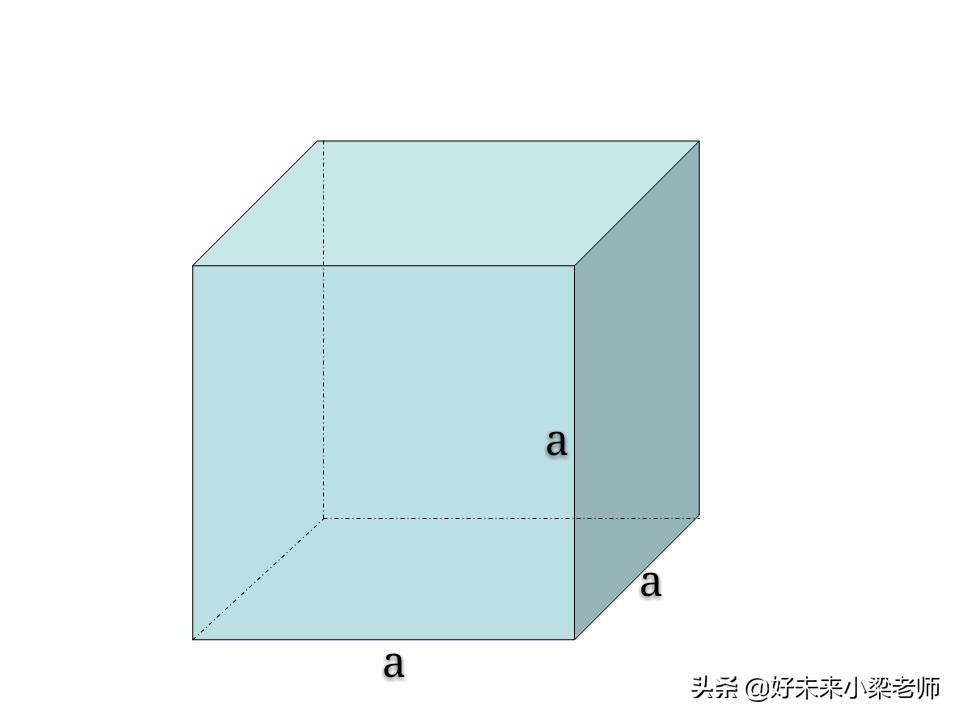
正方体的体积=棱长×棱长×棱长
用字母表示:V=a・a・a
由于三个a相乘,a・a・a=a³(读作a的立方。)
所以正方体公式还可以写成:V=a³
3、长方体和正方体的底面的面积,叫做它们的底面积。
由于长方体的底面积=长×宽
正方体的底面积=棱长×棱长
所以长方体和正方体的体积还可以写成:
长方体(或正方体)的体积=底面积×高
用字母表示:V=Sh
4、体积单位之间换算的由来。
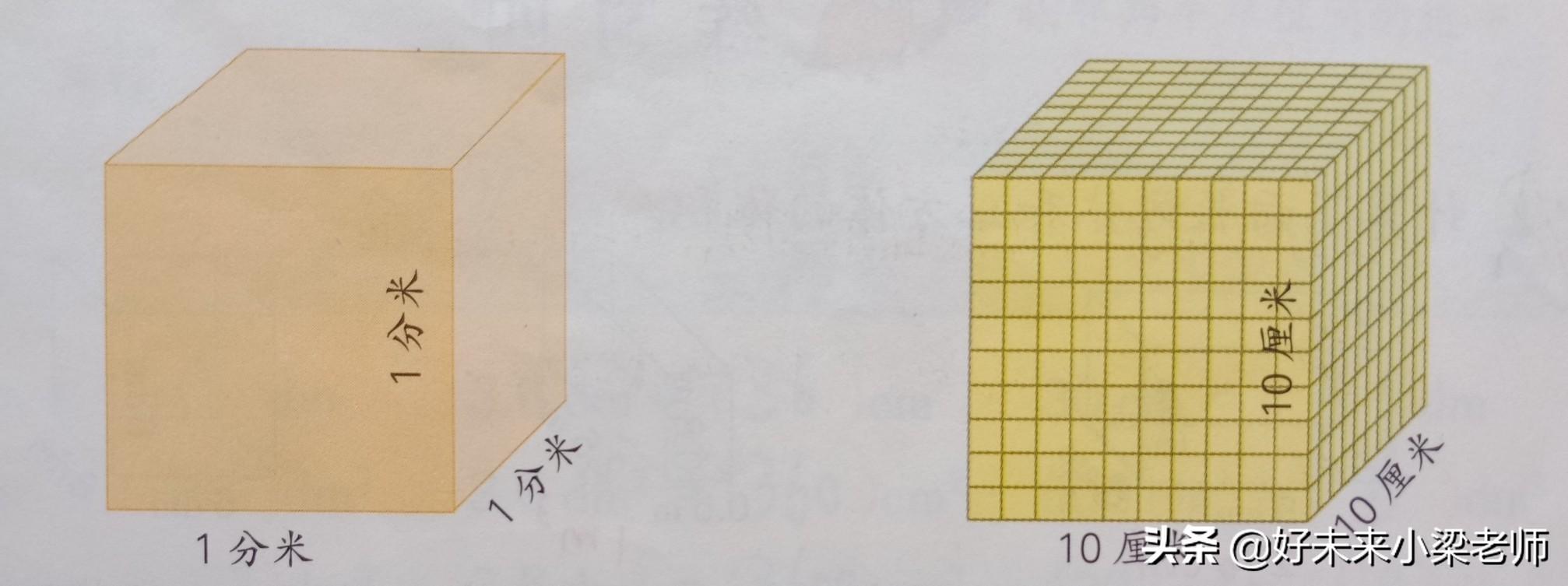
由于1分米=10厘米,所以1立方分米的正方体体积:
1分米×1分米1分米=10厘米×10厘米×10厘米=1000(立方厘米)
也就是:1立方分米=1000立方厘米
同理,1米=10分米,所以1立方米的正方体
1米×1米×1米=10分米×10分米×10分米=1000立方分米。
也就是1立方米=1000立方分米
练习:课后“练习四”所有题目都可以做,有几个实际问题需要特别注意,要按照实际情况计算。
