期中考试已经结束,接下来的第五单元和第六单元是五年级上学期的难点内容,第五单元的解方程问题更是其中一个比较难的一个问题,课本中一共给出了五个例题帮助孩子们来理解和掌握解方程的方法和技巧,但是很多孩子在老师的讲解之后还是似懂非懂的状态,例题看懂了,但是其他的题还是不会做,那么下面我们来分析一下这五个例题,希望对孩子们有所帮助。

例1 :通过给出的图我们可以看出,一共有9个,左边是x个,右边是3个,两者之和就是9,所以可以得到一个式子:x+3=9 。那么这个方程该如何解决呢?我们这里是借助天平来讲解,等号左边相当于天平的左边,等号右边相当于天平的右边,利用等式的型之一:等式两边同时加或者减去相同的数,等号不变。(等式的两个性质一定要熟记掌握)所以两边同时减去3,得到x+3-3=9-3 , 因为要求x是多少,所以可以利用天平把左边已知的3个减去就只剩下x了,所以要减去3,而且是同时减去3.最终得到x=6 。这里要明白方程的解和解方程的区别,方程的解是未知数的具体数值,而解方程是求出方程的解这个数值的过程。还有一个非常重要的点是解方程的最后一步,检验。检验的方法是把求解的答案带回原来的式子检验,也就是方程的左边=x+3=6+3=9=方程的右边,这样就说明我们之前解方程的过程是正确的。例1学习的是利用等式的性质一进行解方程,两边同时加或者减的问题。注意:解方程先写上解、等号要对齐。
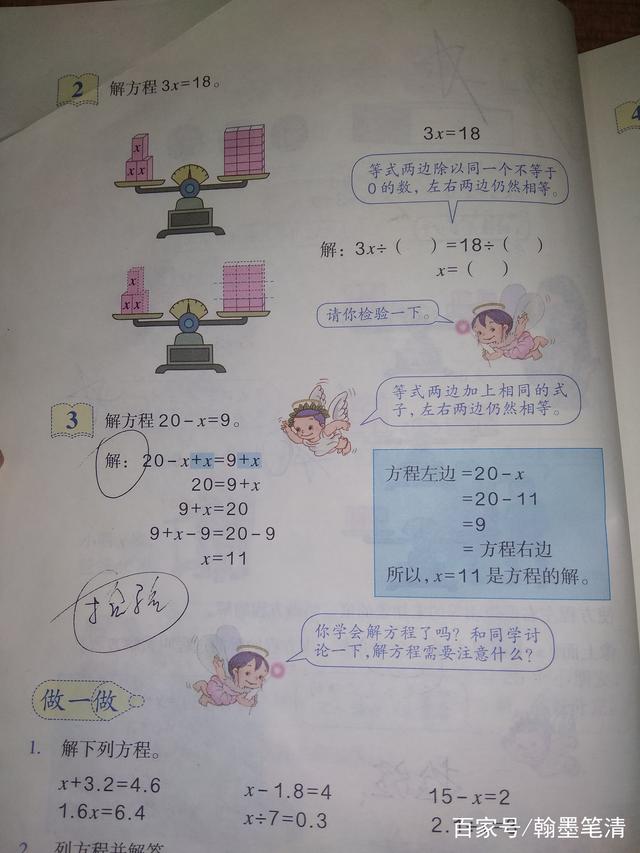
例2:这道题学习的是利用等式性质二进行解决问题。(等式性质二:等式两边同时乘或者除以相同的数(0除外),等号不变。)讲解这道题时候,借助天平这样左边有3个x,求得是一个x,怎么只剩下一个x呢,那么就要把三个变成一个就是除以3,左边除以3,右边同样的也得除以3 。所以得到x=6,得到答案之后别忘了检验一下是否正确,方程左右是否相等。
例3:这道题考查的还是利用等式性质一进行解方程。只是比较特殊一点,x是减数,在减号后边。只要是减法的解方程就一定是两边同时加上减去的数,哪怕减数是未知数,也得加上未知数,所以等式两边同时加上x,转化为20-x+x=9+x 。也就是20=9+x 。一般情况下都是未知数在左边,所以就是9+x=20,再进行解方程即可。
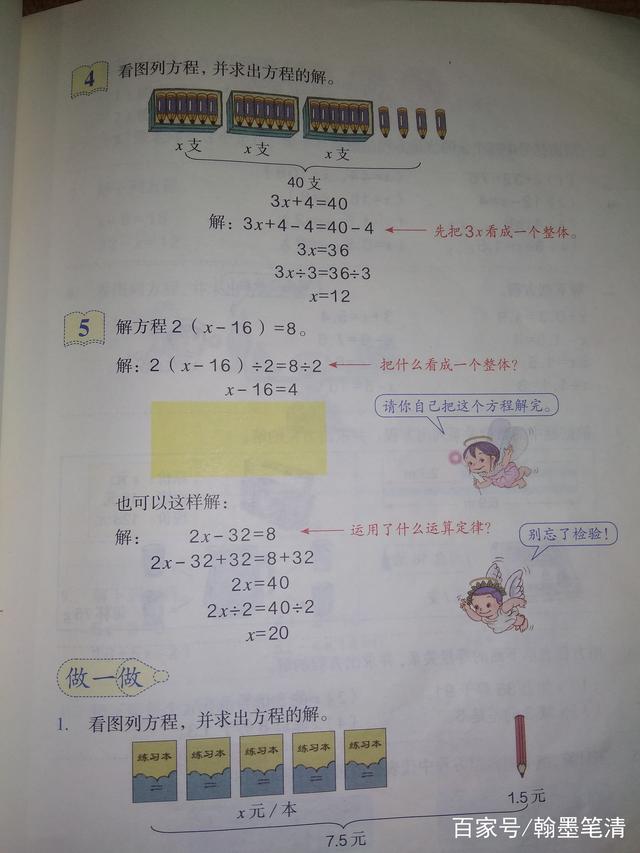
例4:先看图分析图,图中有3个未知数x,所以为3x,还有四个单独的,所以是4.两者之和实40 。那么得到一个方程3x+4=40,这样的方程怎么解呢?一定要明白最终的目的是求x的值,所以想法把左边的3和4去掉,3和x是一起的,不好去掉,所以先把他们两个看成一体,先把容易去掉的4去掉,那么就是利用性质一两边同时减去4,得到3x=36,再利用性质二两边同时除以3,得到x=12 。
例5:2(x-16)=8,这个方程比较复杂,有乘法,有除法,还有括号,那么该怎样解方程呢?要想使左边只剩下x,那么就要去掉左边的2和16,那么16在括号里边不好攻克,那么就先选比较好去掉的2,所以两边同时除以2,得到x-16=4 ,这样再去掉16,那就得两边同时加上16,得到x=20。
解方程有一定的小技巧,我总结了一个小口诀:加用减消,减数字。减用加消,减谁加谁。乘用除消,除以数字。除用乘消,除以谁就乘谁。当然这里加减乘除是看方程的左边,变化的时候要左右同时变化,这样解方程就会变得简单很多,希望对孩子们的学习有所帮助。
