一、基本公式
(1)工作总量=工作效率×工作时间。
(2)工作效率=工作总量÷工作时间。
(3)工作时间=工作总量÷工作效率。
二、基本思路
假设工作总量为“1”(和总工作量无关),即设一个方便的数为工作总量(一般是它们完成工作总量所用时间的最小公倍数),利用上述三个基本关系,可以简单地表示出工作效率及工作时间。
例 1.单独完成某项工作,甲需要 16 小时,乙需要 12 小时。如果按照甲、乙、甲、乙、……的顺序轮流工作,每次 1 小时,那么完成这项工作需要多长时间?()。
A.13 小时 40 分钟 B.13 小时 45 分钟C.13 小时 50 分钟 D.14 小时
例 2.一条公路,甲队单独修建需要 24 天完成,乙队单独修需要 30 天,甲乙两队合作若干天后,乙队停工休息,甲队继续修了 6 天完成,乙队修了多少天?
例 3.单独完成某工程,甲队需 10 天,乙队需 15 天,丙队需 20 天。开始三个队一起干,因工作需要甲队中途撤走了,结果一共用了 6 天完成这一工程。则甲队实际工作了几天?
例 4.一项工程,如果甲先做 5 天,那么乙接着做 20 天可完成;如果甲先做 20 天,那么乙接着做 8 天可完成。如果甲、乙合作,那么多少天可以完成?
例 5.单独完成一件工作,甲按规定时间可提前 2 天完成,乙则要超过规定时间 3 天才能完成。如果甲、乙二人合作 2 天后,剩下的继续由乙单独做,那么刚好在规定时间完成。则甲、乙二人合做需多少天完成?
例 6.小李计划用若干天完成某项工作,在小李独立工作两天后,小王加入此项工作,且小李和小王的工作效率是相同的,结果提前两天完成了任务,则小李原计划用()天来完成此项工作。
A.6 B.8 C.10 D.12
参考答案:
例 1.B
例 2.10 天
例 3.3 天
例 4.
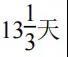
例 5.6 天
例 6.A

