一、数学期望的由来

在17世纪，有一个赌徒向法国著名数学家帕斯卡挑战，给他出了一道题目：甲乙两个人赌博，他们两人获胜的机率相等，比赛规则是先胜三局者为赢家，一共进行五局，赢家可以获得100法郎的奖励。当比赛进行到第四局的时候，甲胜了两局，乙胜了一局，这时由于某些原因中止了比赛，那么如何分配这100法郎才比较公平？

用概率论的知识，不难得知，甲获胜的可能性大，乙获胜的可能性小。

因为甲输掉后两局的可能性只有(1/2)×(1/2）=1/4，也就是说甲赢得后两局或后两局中任意赢一局的概率为1－(1/4)=3/4，甲有75%的期望获得100法郎；而乙期望赢得100法郎就得在后两局均击败甲，乙连续赢得后两局的概率为(1/2)*(1/2)=1/4，即乙有25%的期望获得100法郎奖金。

可见，虽然不能再进行比赛，但依据上述可能性推断，甲乙双方最终胜利的客观期望分别为75%和25%，因此甲应分得奖金的100*75%=75(法郎)，乙应分得奖金的的100×25%=25(法郎)。这个故事里出现了“期望”这个词，数学期望由此而来。

二、数学期望定义

日常生活中，我们每做一件事，都有对它的期望，这里的期望不仅仅只结果的胜负之类，也可以与状态有关。在概率论和统计学中，一般指的就是达到结果的期望，最朴素的计算是每次可能结果的概率乘以其结果的总和。它反映随机变量平均取值的大小。

这是最基本的数学特征。

广义下的定义：一次随机抽样中所期望的某随机变量的取值。

数学期望(mathematic expectation[4])（或均值，亦简称期望）定义：

三、数学期望的应用

在实际应用中，数学期望可以用来解决各种问题，包括经济、金融、物理学、工程学等。是所有管理决策的过程中，尤其是在金融领域是最实用的统计工具。某个事件（最初用来描述买彩票）的期望值即收益，实际上就是所有不同结果的和，其中每个结果都是由各自的概率和收益相乘而来。

假设你参与了一个掷骰子的游戏，游戏规定掷出1点可以获得1元，2点可以获得2元，以此类推。那么在这个游戏中，掷一次骰子的期望值是多少?每一个结果都有1/6的概率，因此期望值为：

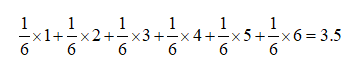
大致一看，3.5元似乎是一个无效数据，毕竟你不可能掷一次骰子就获得3.5元，但事实上，期望值是一个非常有用的参考数据，通过比较成本投入和期望收益，你就能知道做这件事是不是“值得”。比如，还是上述的掷骰子游戏，每玩一次需要缴纳3元，你还玩吗？当然，因为期望回报（3.5元）会高于游戏成本（3元）。这虽然并不代表你每一次玩都能保证赚到钱，但至少可以帮助你认清哪些事情值得冒险。

四、遵循“大数定律”

概率论里有一个与期望相关的定律叫做大数定律，即随着实验次数的增多，结果的平均值会越来越接近期望值。大数定律可以解释很多问题，比如为什么赌场从长期来看总是挣钱：赌场内所有项目的概率都是有利于赌场老板的（出“老千”的赌客不考虑在内）。如果赌场的营业时间足够长，吸引到下注人数也足够多，那么赌场从赌桌赚到的钱肯定要比付出的多。

再比如保险行业。整个保险行业都是建立在概率的基础之上，公司愿意承担风险的原因很简单：如果保险公司制定的保费标准正确合理，从长期来看将会给公司带来不菲的收益。假设车的赔偿额度为20万元，每年被盗的概率是万分之一，那么该车的年预期损失为20元，车险保费组成中盗窃险种的定价就应该高于20元，虽然需要付出，但从长期来看，得到的肯定要比付出的多。从统计学的角度来看，购买保险绝对是一个“糟糕的投资”，但保险能为你做的是，在你遭遇一些难以承受的巨大损失时，为你提供赔付，帮你渡过难关。

四、数学期望的特点

用数学期望衡量长期价值也有一个前提，就是所有随机出现的结果都必须数值化，也就是变成一个具体的数，只有这样，我们才能计算。

比如你问“回老家工作好，还是留北京工作好”，如果只停留在“留北京工作机会多，但竞争压力大；回老家生活压力小，但发展机会少”这些条件上，就没法计算数学期望。只有赋予每个结果具体的数字，比如工作机会多对自己很重要，打10分；竞争压力小对自己没那么重要，打5分……这个问题才真正变得可以比较，这也是数学思维的好处。

前面我们说计算数学期望要对具体事项赋予相应的数值才能计算，就这个赋值的过程是个体的、个性的。每个人对于同一件事所赋予的值是不一样的，计算出的数学期望对每个个体来说，就都是不一样的。这种个体的主观考量，只影响数学期望的计算结果，而不妨碍数学期望起作用。