01角平分线的相关知识点
1、角平分线:从一个角的顶点引出来一条射线,把这个角分成两个相等的角,这条射线叫做这个角的角平分线。
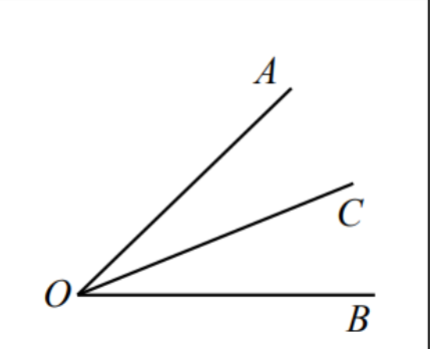
如下图,射线OC平分∠AOB,则∠AOC=∠BOC=∠AOB(或∠AOB=2∠AOC=2∠BOC)。
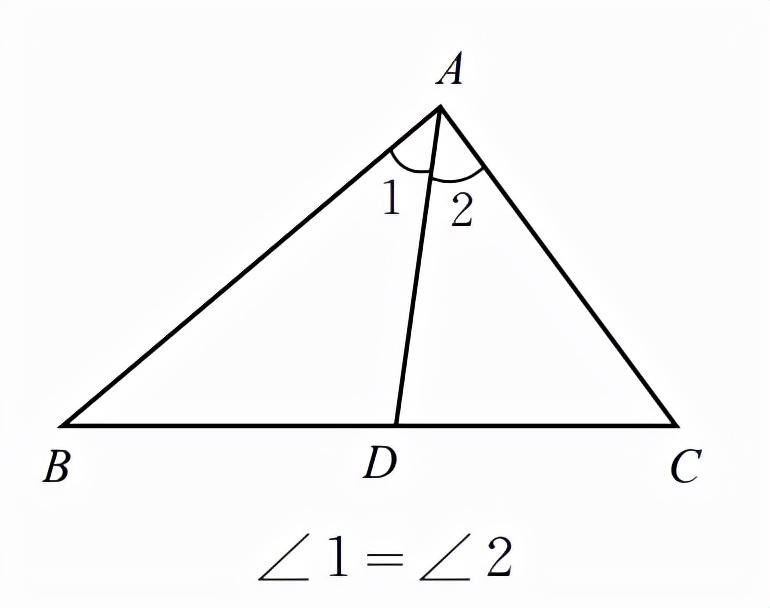
2、三角形的角平分线:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。三角形的三条角平分线交于一点,叫做内心。如下图,AD是ABC的一条角平分线。
3、角平分线的性质定理:角平分线上的点到角两边的距离相等。

4、角平分线的判定定理:在一个角的内部,到角的两边距离相等的点在这个角的角平分线上。


知识总结:
当题干中出现角平分线时,首先标注相等的角,然后记得使用角平分线上的点到角两边的距离相等。
02角平分线的相关模型
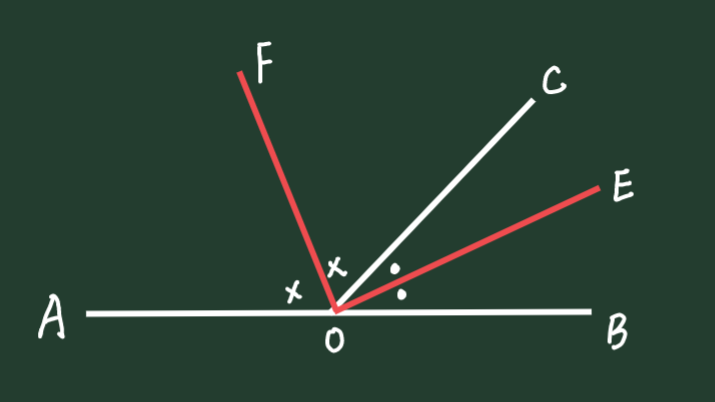
1、如下图,∠AOB为平角,射线OC把平角分∠AOC和∠AOB,射线OF平分∠AOC,射线OE平分∠BOC,则两条角平分线的位置关系为OF⊥OE。
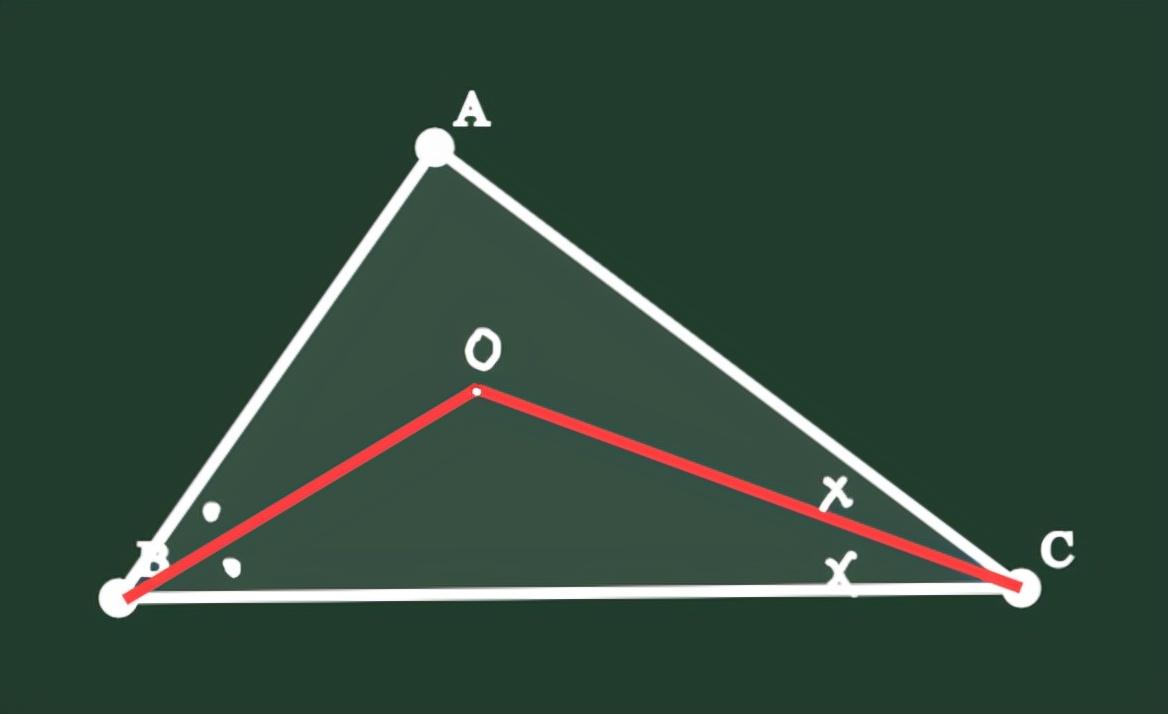
2、如下图,在ABC中,OB平分∠ABC,OC平分∠ACB,两条角平分线交于点O,则∠O=90°+∠A。
3、如下图,在在ABC中,OB平分∠ABC,OC平分∠ACB的相邻外角∠ACD,两条角平分线交于点O,则∠O=∠A。
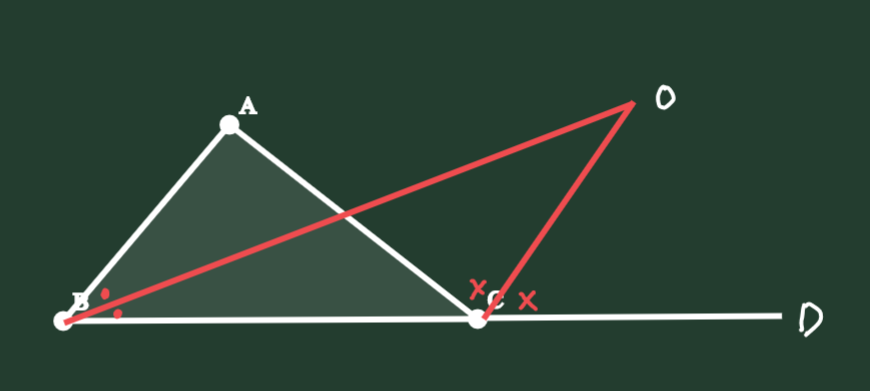
4、如下图,在ABC中,OB平分∠EBC,OC平分∠DCB,两条角平分线交于点O,则∠O=90°-∠A。
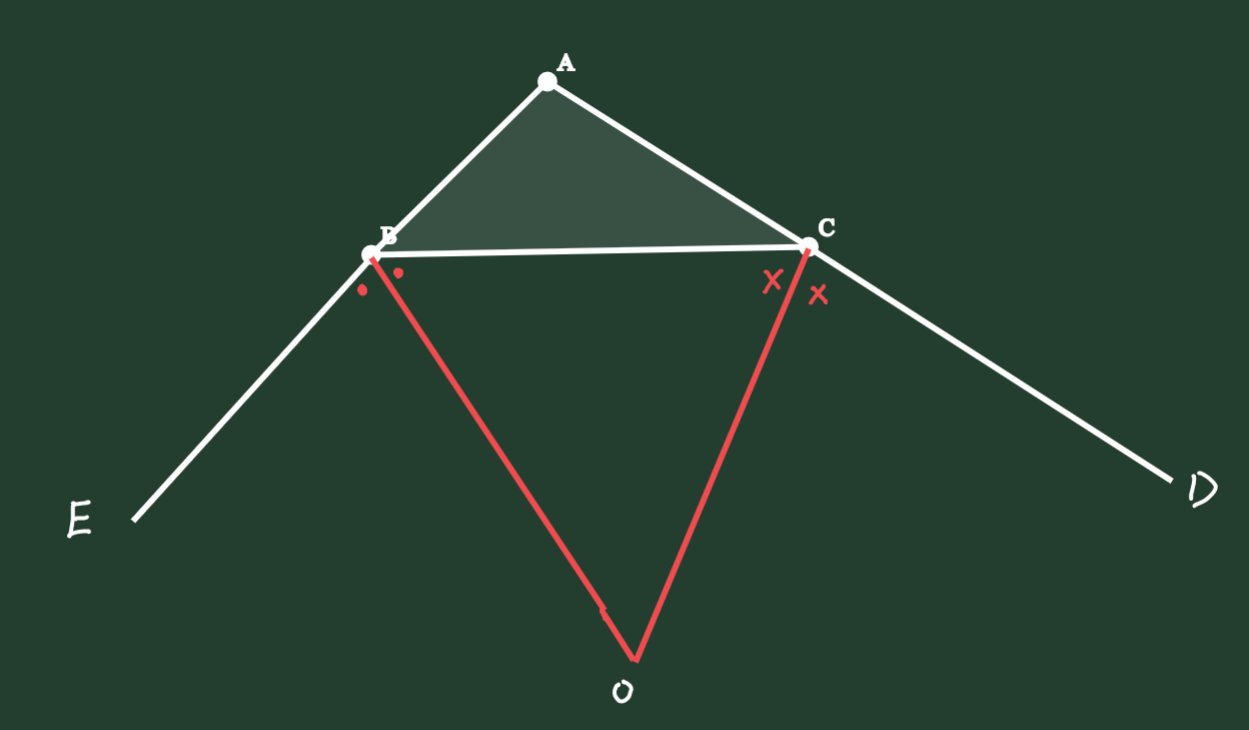
03与角平分线有关的辅助线
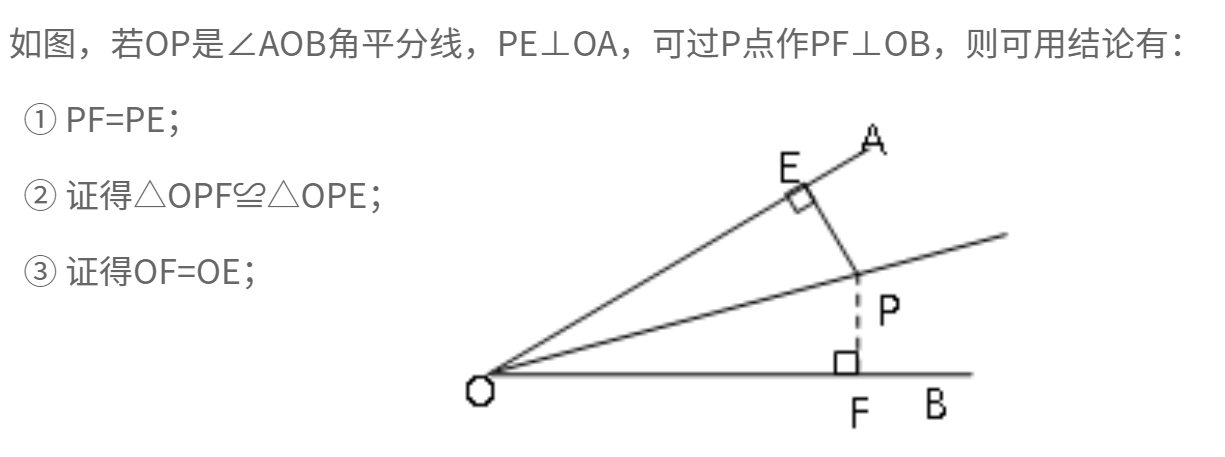
1、点在平分线,可作垂两边
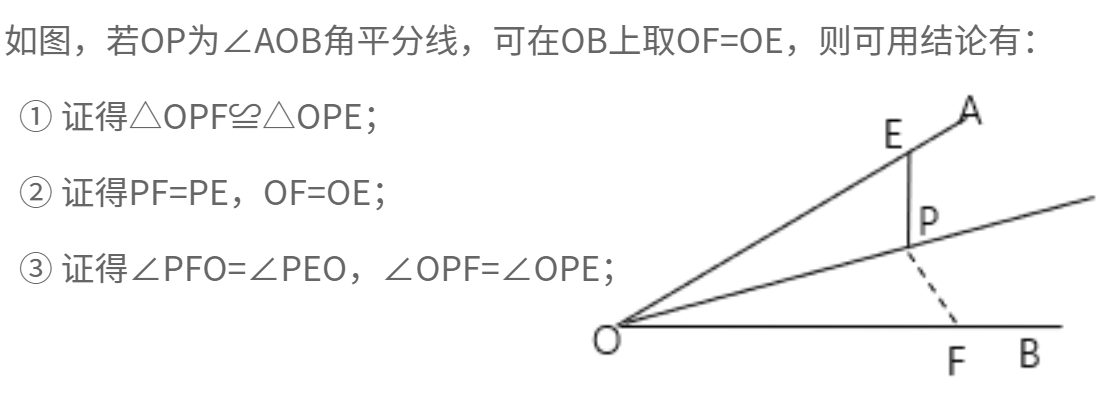
2、角边相等,可造全等
3、平分加平行,可得等腰形(常关联截长补短法构造三角形全等)
①过角平分线上一点,作角的一边平行线,可构得等腰三角形。

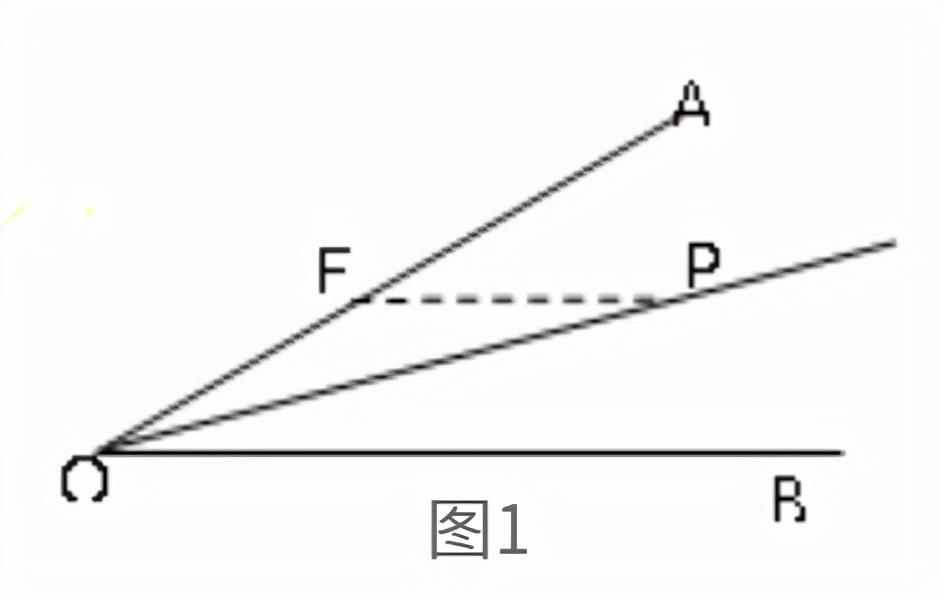

②过角的一边上的一点,作角平分线的平行线,可构等腰三角形。
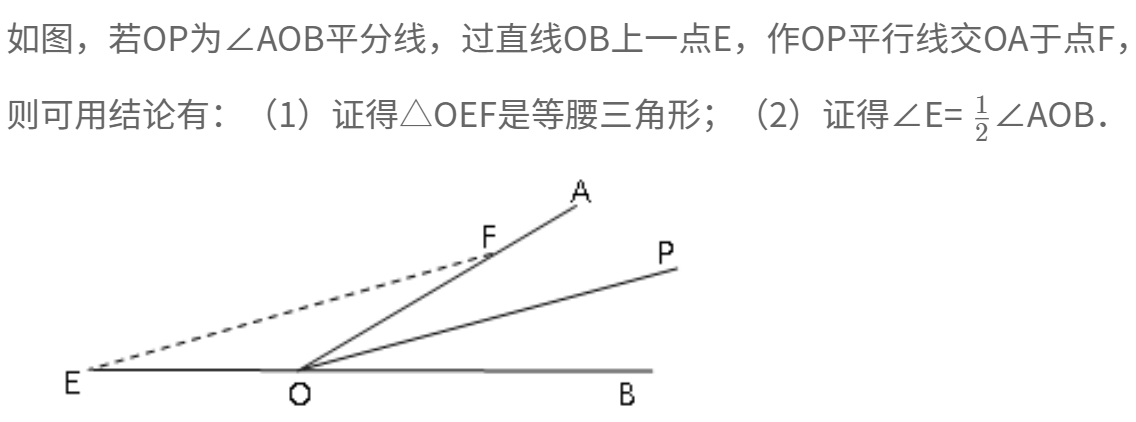
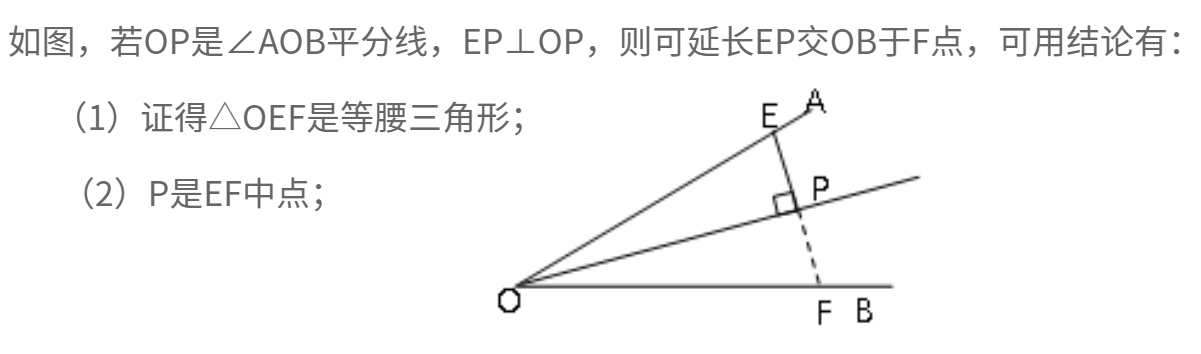
4、平分加垂线,补得等腰现
从角的一边上一点作角平分线的垂线,与另一边相交,可得等腰三角形。
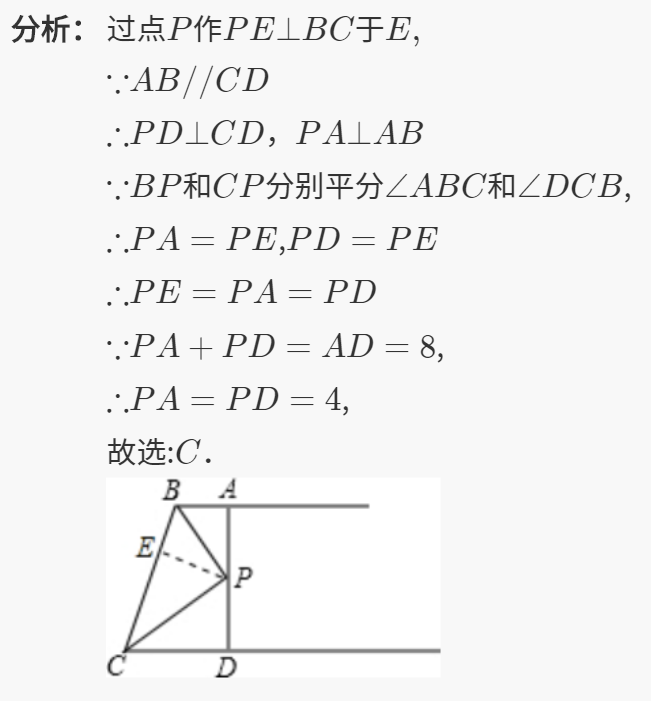
04真题分析



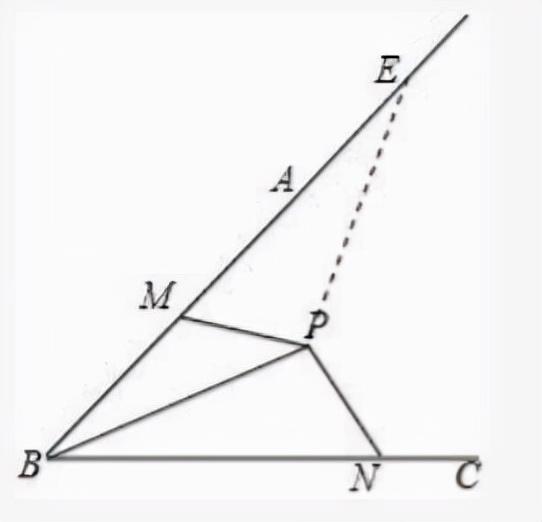






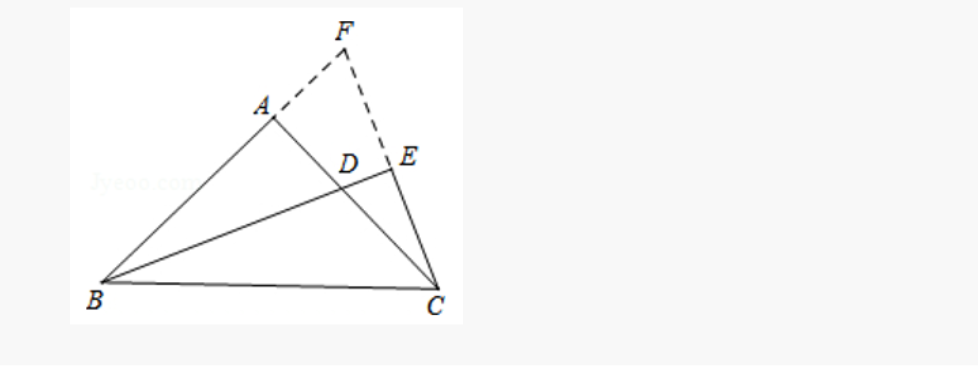
05总结
以上角平分线的模型及相关辅助线,其中最主要的是:①标注等角;②过角平分线上点向角两边作垂线;两部完成之后,不仅有了相等的角,还有了相等的边,接下来就可以做等量代换,接着去分析。上面的知识点需要做好积累,多复习巩固!
