我们先来看第一种情况:多个函数进行四则运算的导数。
函数四则运算求导法则
我们假设 u = u(x) 和 v = v(x) 都在x点有导数,那么它们进行加减乘除四则运算之后的结果的导数有如下性质:
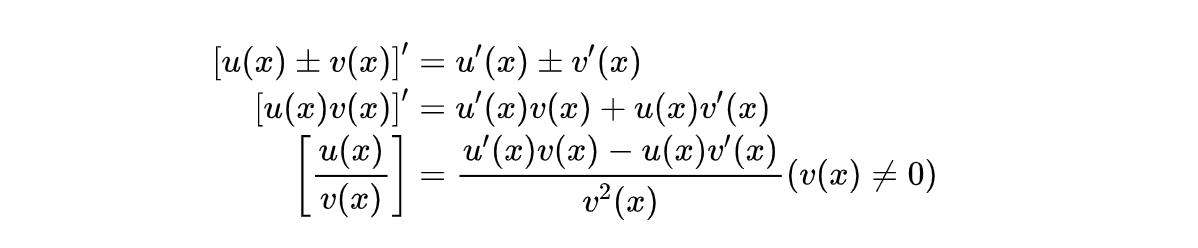
我们来看一下证明过程,熟悉证明过程并不是炫技,除了能加深对公式的理解之外,更重要的是防止遗忘。即使以后真的不记得公式的细节了,也可以临时推导一下,这是学算法和数学很重要的技巧。
我们先来看第一个,第一个很容易证明,我们直接套一下导数的公式即可:
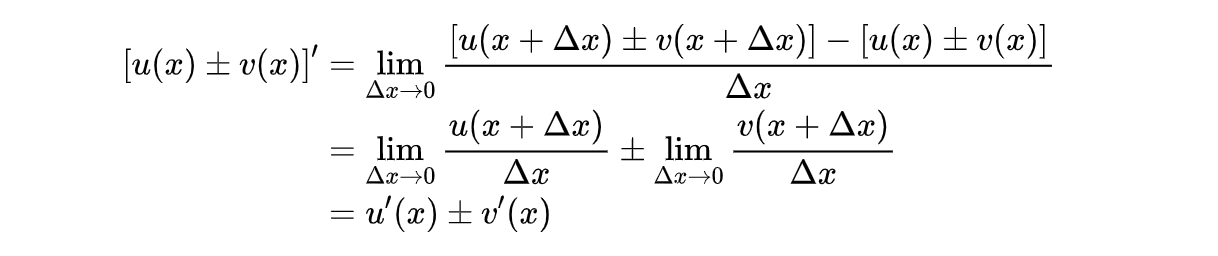
第二个式子同样套用公式:
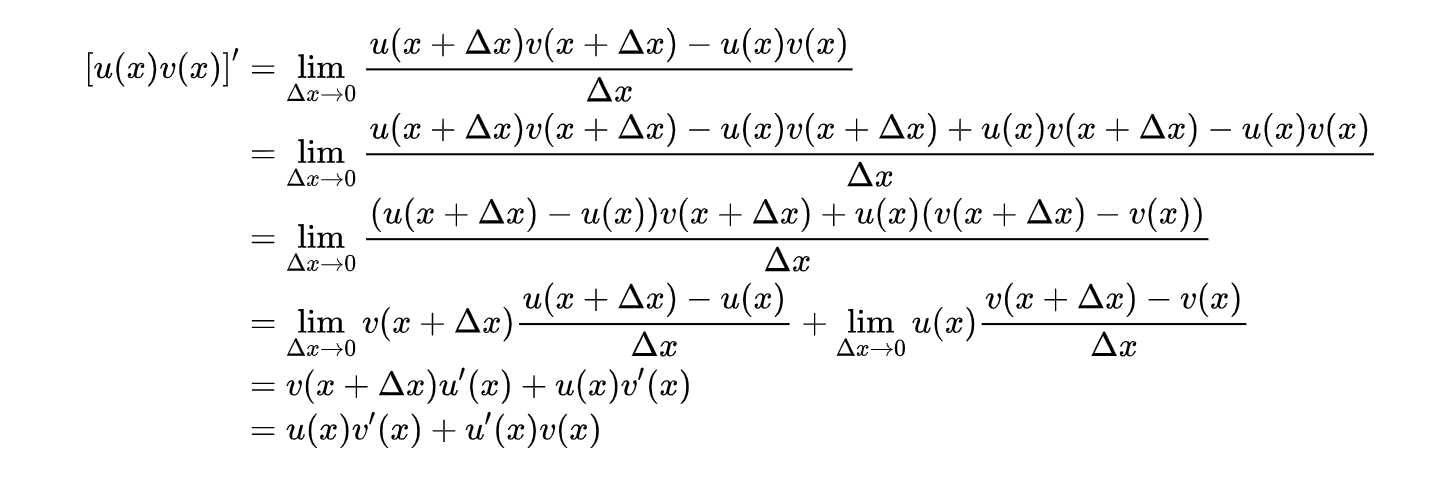
最后是第三个式子的推导,也并不复杂:
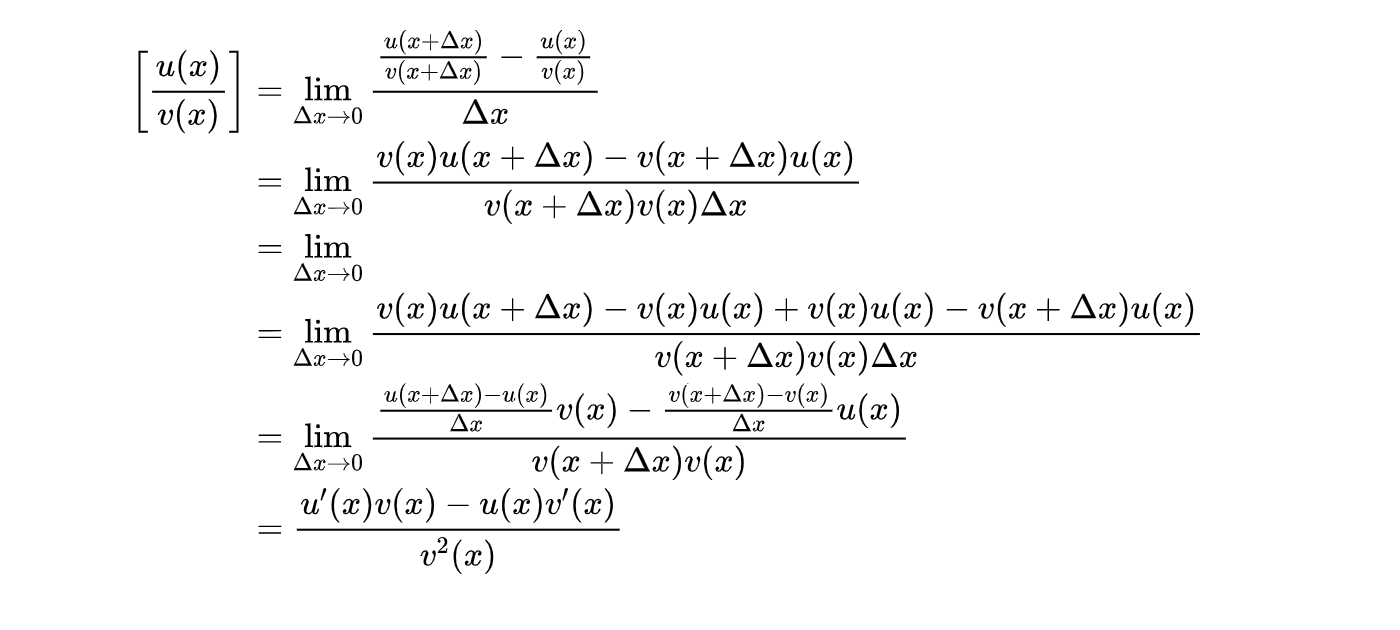
反函数求导法则
推导完了四则运算的求导法则,我们再来看一下反函数的求导法则。
我们陷在了看结论,如果函数 x = f(y) 在区间 Iy 内单调、可导并且 f'(x) != 0,那么它的反函数
在区间 Ix = {x | x = f(x), y ∈ Iy} 内也可导,那么:
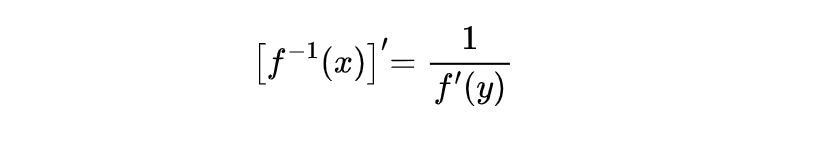
关于这个结论的证明很简单,因为 x = f(y) 在区间内单调、可导,所以它的反函数存在,并且也单调且连续。
所以:
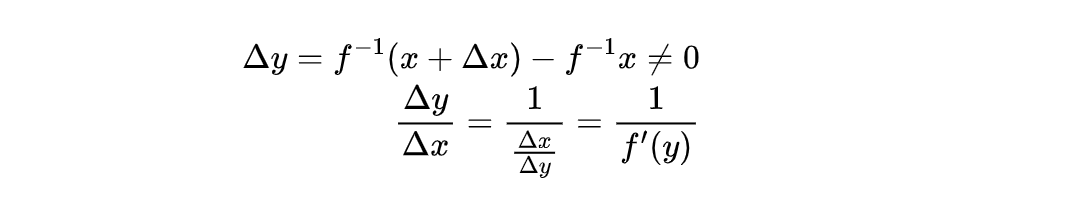
由于反函数连续
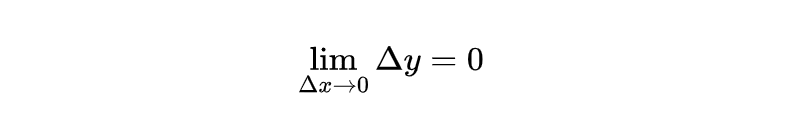
所以上式成立。
我们来看一个例子:
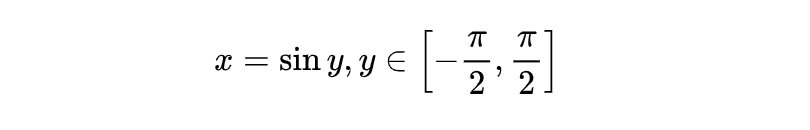
则
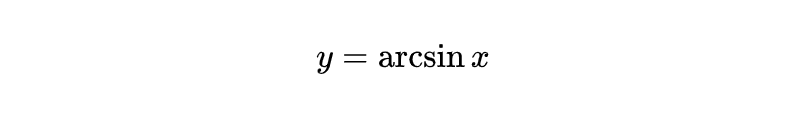
是它的反函数,根据上面的公式,我们可以得到:
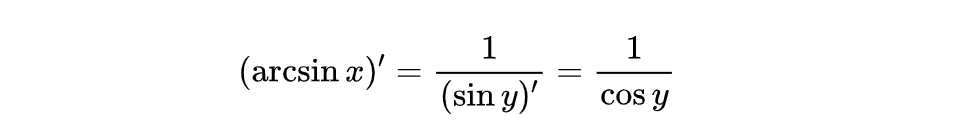
由于
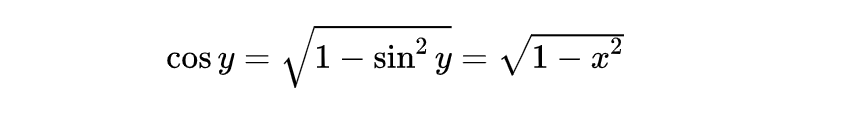
代入上式可以得到:
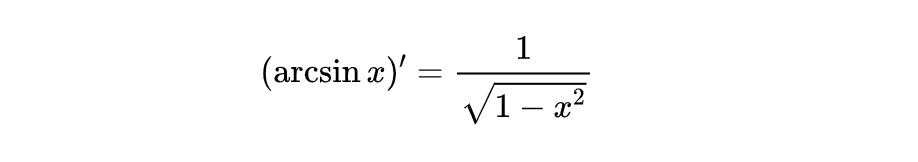
利用同样的方法,我们还可以求出其他反三角函数的导数,由于这些并不太常用,所以我们就不多介绍了,感兴趣的同学可以自己利用导数的定义推导一下,我想应该也不难。
复合函数求导
这是最后一个法则,也是本篇文章的重点,因为经常用到。我们现在已经搞定了一些常见的函数,还搞定了常见函数加减乘除之后求导的结果,但是对于一些看起来比较复杂的函数,我们并不能一下写出它们的导数。
比如说:sin(x^2+3x) ,比如 ln(3x+1)等等,这些函数基本上都可以确定是连续并且可导的,但是我们一下子并不能写出它们的导数,而且要通过导数的定义推导也非常麻烦,对于这些导数就需要用到今天的重头戏,也就是复合函数的求导法则了。
对于复合函数而言,拥有如下法则:如果函数 u = g(x) 在点x处可导,并且 y = f(u) 在点 u = g(x) 处也可导,那么复合函数 y = f[g(x)] 在x处可导,它的导数为:
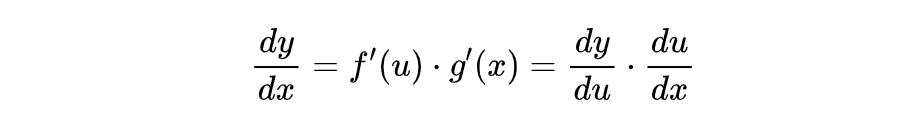
如果复合函数的数量更多也是一样的,我们按照顺序依次相乘即可。由于公式的形式像是一根链条一样依次所以,复合函数求导法则也叫链式求导法则。在举例之前,我们先来证明一下。
由于 y = f(u) 在点u处可导,因此
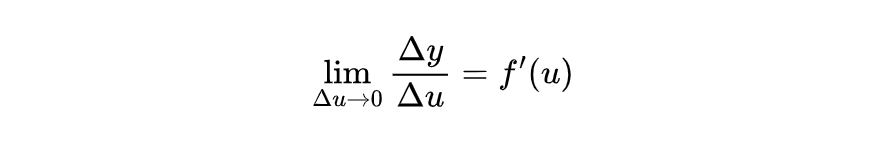
因为 f'(u) 存在,所以我们将它变形为:
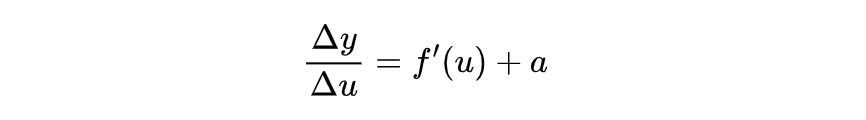
其中a是 Δu 趋向于0 时的无穷小,我们对两边同时乘上 Δu ,可以得到:
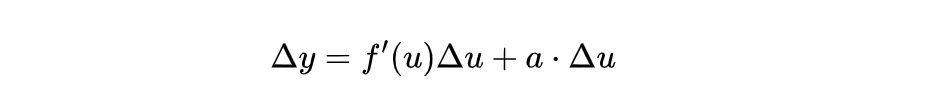
上式当中 Δu 和a都是无穷小,所以当 Δu 趋向于0 时,Δy = 0,我们对上式两边同时除以
Δx ,得:
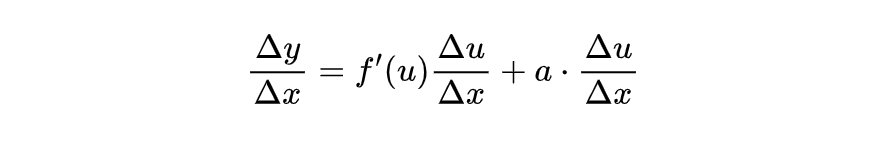
于是:
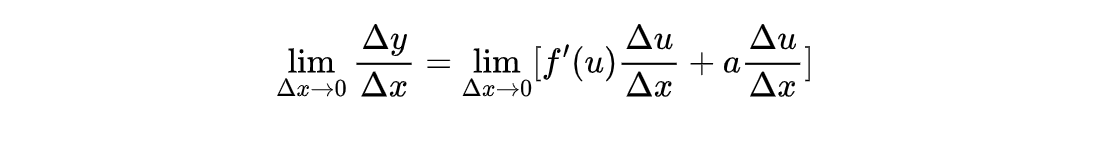
又根据 u = g(x) 在点x处可导,所以有:
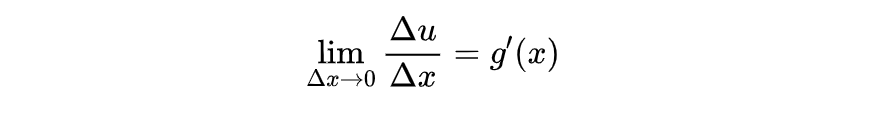
我们代入,就可以得到:
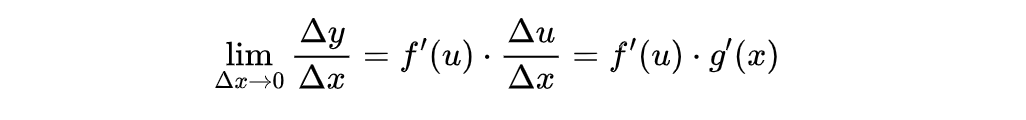
其实我们都知道相比于公式的证明,公式的运用更加重要,下面我们就来看两个例子,来巩固一下这个链式求导法则: y = lnsin3x ,求 y'
我们令 u = 3x, g = sinu
所以:
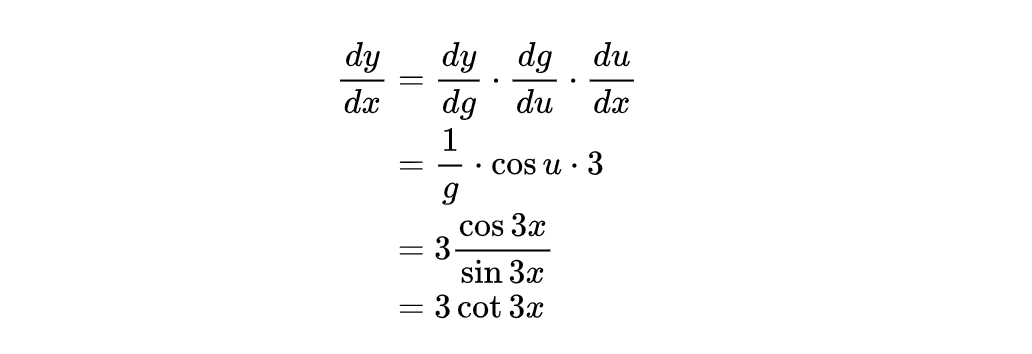
再举个例子,还记得我们之前推导线性回归时候用到的均方差的公式吗:
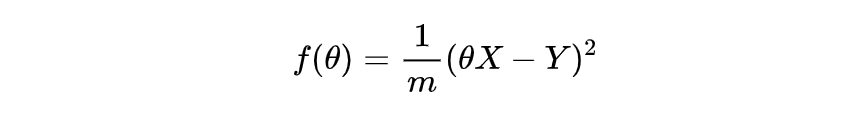
我们来试着学以致用,求一下 f(θ) 的导数,在机器学习当中,X和Y都是样本都是已知的参数,要求的是 θ ,所以我们对 θ 求导:
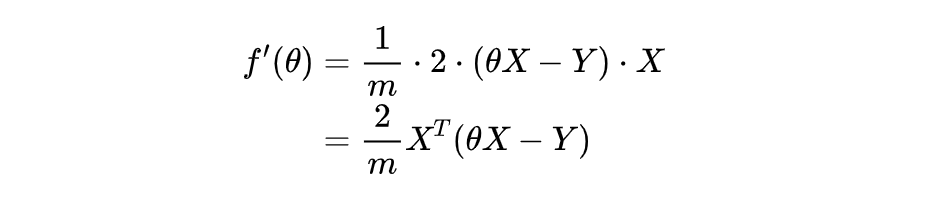
这个结果其实就是之前我们说的梯度,梯度本来就是由导数计算得到的,所以理解了链式求导的公式,可以再回过头看看之前线性回归和梯度推导的公式,相信会有更深刻的体会。
