说到全微分,想必大家应该都知道概念,所谓的全微分就是对多元函数的每个未知量都要求偏导,然后再做加法。
全微分的定义:如果函数z=f(x, y) 在(x, y)处的全增量Δz=f(x+Δx,y+Δy)-f(x,y)。
表示为Δz=AΔx+BΔy+o(ρ),其中A、B不依赖于Δx, Δy,仅与x,y有关,ρ趋近于0(ρ=√[(Δx)2+(Δy)2]),此时称函数z=f(x, y)在点(x,y)处可微,其中AΔx+BΔy称为函数z=f(x, y)在点(x, y)处的全微分,记为dz=AΔx +BΔy。
表达式dz=AΔx +BΔy称为函数z=f(x, y) 在(x, y)处关于Δx, Δy的全微分。
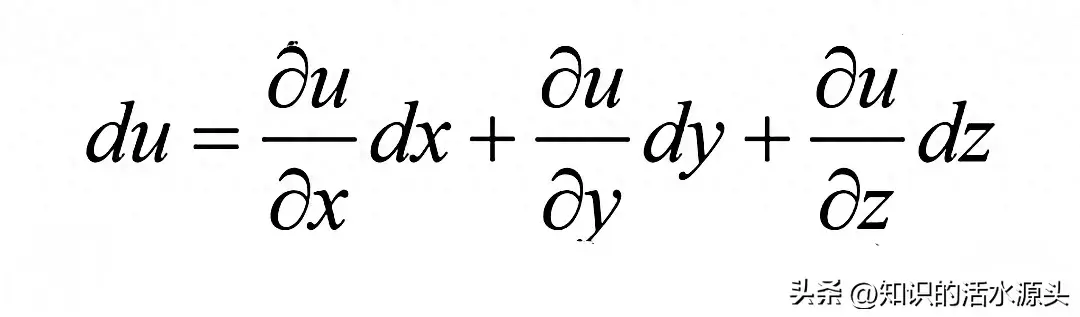
我们来看一个例题:

通过题目,我们可以看出来,该函数类似于指数函数模型,在求解在某点处全微分,必须要先进行求解偏导。
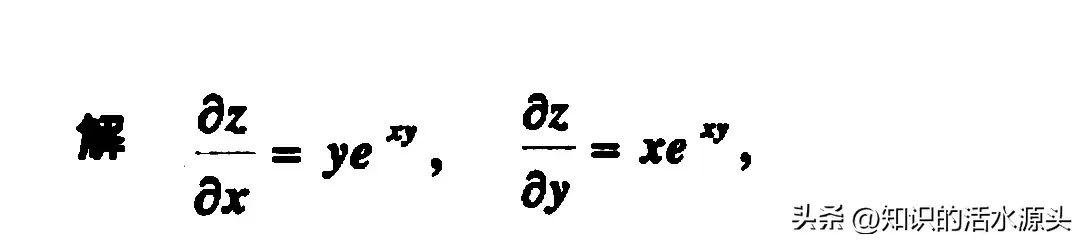
分别对x和y进行求偏导,得到以上步骤,在求解偏导时,要注意的是,把其中一个未知量看成常数。然后再根据底数为e的指数函数求导即可。
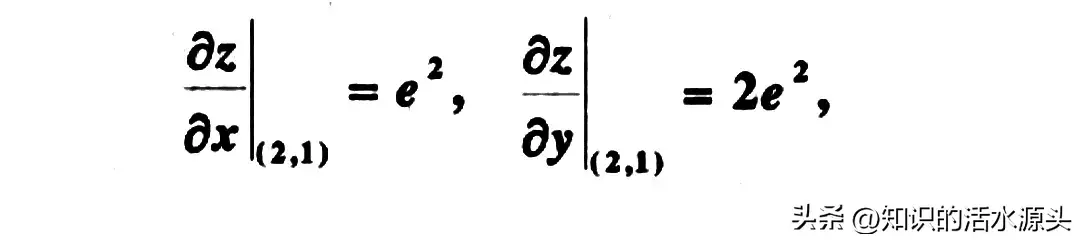
偏导求解完成过后,将坐标点代入求出的偏导,求出最终答案即可。
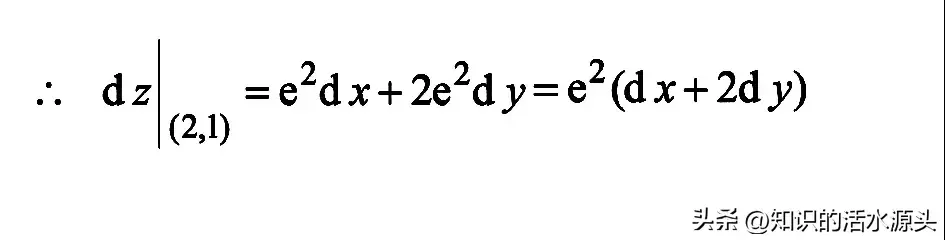
大家可以根据上面讲解的步骤,做一做下面几个练习题。

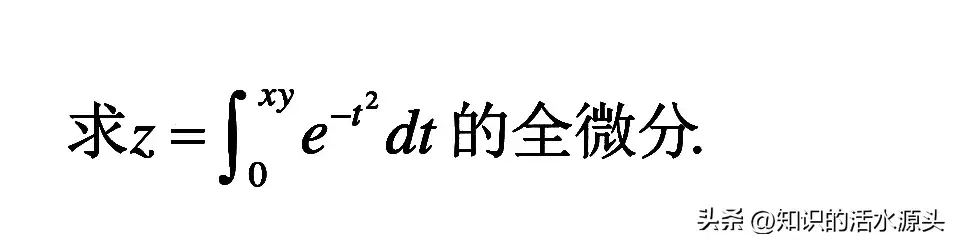
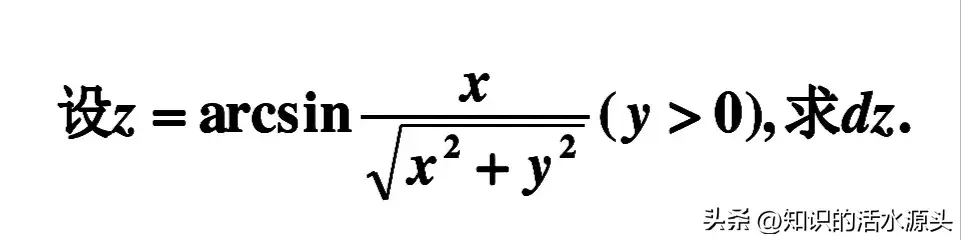
我们再来看一下,全微分要在什么情况下才成立呢?我们一起来看一下他的充分条件,必要条件,以及充分必要条件是什么?
充分条件:要想全微分存在,那么必须满足偏导数连续。
必要条件:要想全微分存在,那么偏导数必须存在。
充要条件:曲面在该点处要具有切平面。

处此之外,我们再来看一下有关全微分求解近似值的方法。

根据定义,我们可以看出,求近似值的公式,也是和偏导数有很大联系的,所以说大家一定要掌握求偏导的方法。
我们来一起看一个例题,熟悉一下。

计算上述这个数的近似值,大家会发现,这个数根本不可能硬算,直接笔算是不可能的,如果要求我们必须计算的话,那么我们可以借助上述表达式进行计算。
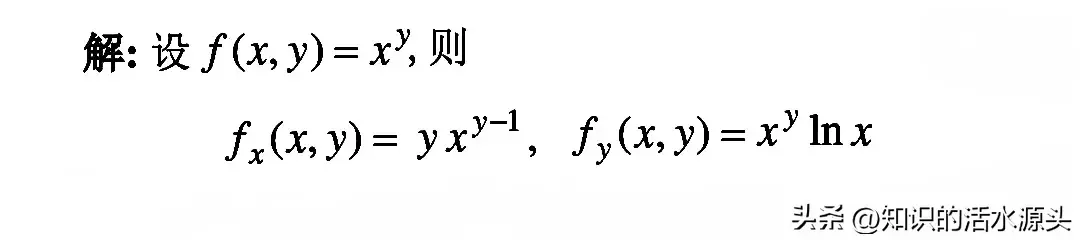
通过观察,我们可以吧上面的这个数,看成是一个幂指函数,通过这个函数,我们可以求出该函数的偏导数。
(幂指函数求偏导数有不懂的可以留言,下次我专讲一个有关幂指函数求偏导的视频)。
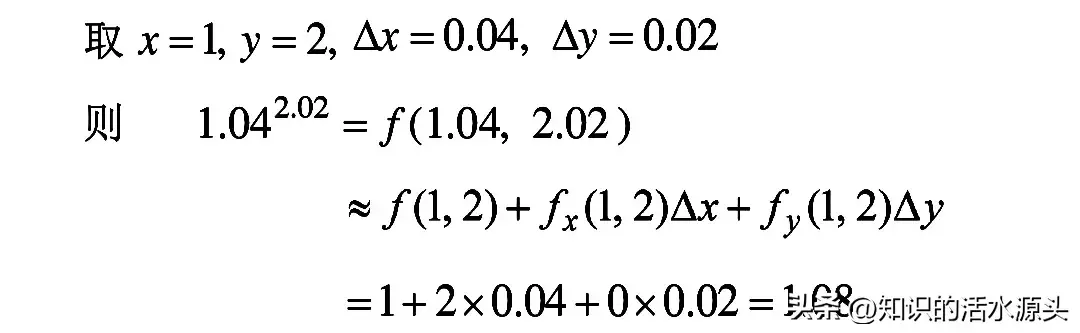
求出偏导,此时我们可以将上面的数分成x和y的两个数,并且将Δx,Δy用最小数将其表达出来。然后代入公式即可得到答案。
