工程问题是小学阶段比较复杂的一类应用题,是学多同学比较头疼的一类应用题。对于简单的题型,直接套用“工作效率、工作时间、工作总量”的关系即可解决,对于复杂的题型,则必须理清楚题目中各种已知数据之间的关系。本文重点介绍一种处理复杂工程问题的方法——列表法。

一、什么是工程问题?
工程问题就是解决关于“工作效率、工作时间、工作总量”的应用题,其中工作效率、工作时间都是隐性条件,不直接给出,只明确告知工作时间。初学时会觉得缺条件,不好做。
工作效率:单位时间内完成的工作量,比如1天或1小时完成了多少工作。
工作时间:完成工作所需的时间。
工作总量:工作时间内完成的总的工作量。
三者之间的关系:
工作效率×工作时间=工作总量
工作效率=工作总量÷工作时间
工作时间=工作总量÷工作效率
二、解决工程问题的方法
1、利用量来求(设数代入法)
2、利用率来求(复杂的用列表法)
例1、(难度等级★)一件工程,甲单独完成需要5天,乙单独完成需要7天,甲乙合作,需要几天完成?
方法一:设数代入法
假设这件工程是修路,全长35千米。
甲每天修:35÷5=7(千米)
乙每天修:35÷7=5(千米)
甲乙合作每天修:7+5=12(千米)
甲乙合作需要的时间:35÷12=35/12(天)
答:甲乙合作,需要35/12天完成。
方法二:
工作总量看作单位“1”
甲的工作效率:1÷5=1/5
乙的工作效率:1÷7=1/7
甲乙合作的工作效率:1/5+1/7=12/35
甲乙合作需要的时间:1÷12/35=35/12(天)
答:甲乙合作,需要35/12天完成。
小结:①方法一设数字时可以设任意数,一般设甲乙工作时间的公倍数,方便计算。②方法二其实也是设了单位“1”,只是通常省略不写。方法二中甲乙的工作效率求解过程也通常省略不写,写出来是为了方便理解每一个数据到底是怎么来的,只有在理解的基础上才能更好地解决复杂的工程问题。③至于最后的结果写成假分数或带分数都可以,以前强调最终结果必须写成带分数,现在一般不作要求(除非题中特别说明)。
例2、(难度等级★★)一项工程,甲单独完成需要30天,甲乙合作需要12天,如果乙单独完成需要多长时间?
方法一:
假设是修路工程,全长60千米。
甲每天修路:60÷30=2(千米)
甲乙合作每天修路:60÷12=5(千米)
乙每天修路:5-2=3(千米)
乙单独完成所需时间;60÷3=20(天)
答:乙单独完成需要20天。
方法二:
乙的工作效率:1/12-1/30=1/20
乙单独完成所需时间:1÷1/20=20(天)
答:乙单独完成需要20天。
小结:本例题按常规写法来写,把方法二设单位“1”和求工作效率的步骤都省略,可以看出方法二比方法一要简洁得多,但是方法一更易于理解。
例3、(难度等级★★★)一件工作,甲乙两人合作30天可以完成,共同做了6天后,甲因有事先离开了,由乙继续做了40天才完成。如果这件工作由甲单独完成需要多少天?
方法一:
假设是修路工程,全长120米。
甲乙合作每天修路:120÷30=4(米)
合作6天修路:4×6=24(米)
乙单独修路:120-24=96(米)
乙每天修路:96÷40=2.4(米)
甲每天修路:4-2.4=1.6(米)
甲单独完成需要的时间:120÷1.6=75(天)
答:甲单独完成需要75天。
方法二:
问题较复杂不知从何入手时,可以把所有已知的工作效率、工作时间、工作总量列出来,然后利用三者的关系把未知的求出来。
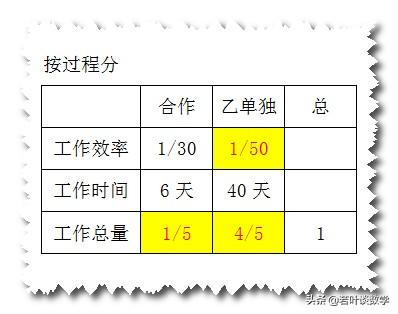
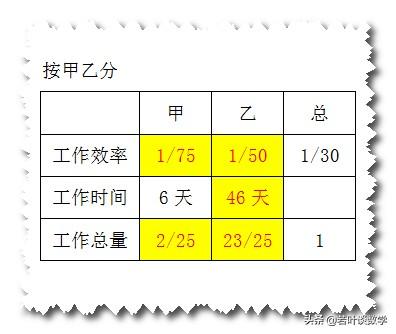
合作6天工作总量:1/30×6=1/5
乙单独做40天工作总量:1-1/5=4/5
乙的工作效率:4/5÷40=1/50
甲的工作效率:1/30-1/50=1/75
甲单独完成需要的时间:1÷1/75=75(天)
答:甲单独完成需要75天。
小结:当问题比较复杂时,两种方法书写步骤差不多,可根据自己的喜好选择合适的方法。总的来说,用量求易理解,用率求较简洁。用率求时,除了上面的方法外,还可以由已知关系先求甲乙工作效率之比,过程如下:甲乙继续合作需要30-6=24(天),现在甲少做24天,乙多做40-24=16(天),说明甲24天的工作量=乙16天的工作量,乙30天的工作甲完成需要30×24/16=45(天),甲单独完成共需要30+45=75(天),理解起来稍复杂。
总结
1、小学阶段缺条件的应用题都可以用“设数代入法”来解决;
2、设单位“1”是设数代入法的特殊情形,一般情况下无需特别说明,可以直接用;
3、较复杂的应用题常借助画图、列表、列关系式等方法来帮助理解题意,理清题中数量关系;
4、有序思维(其实就是逻辑思维),解题时要遵循一定的思路,要有大致的解题方向,不能竹竿打枣——横竖乱扫;
5、虚怀若谷、熟能生巧。
