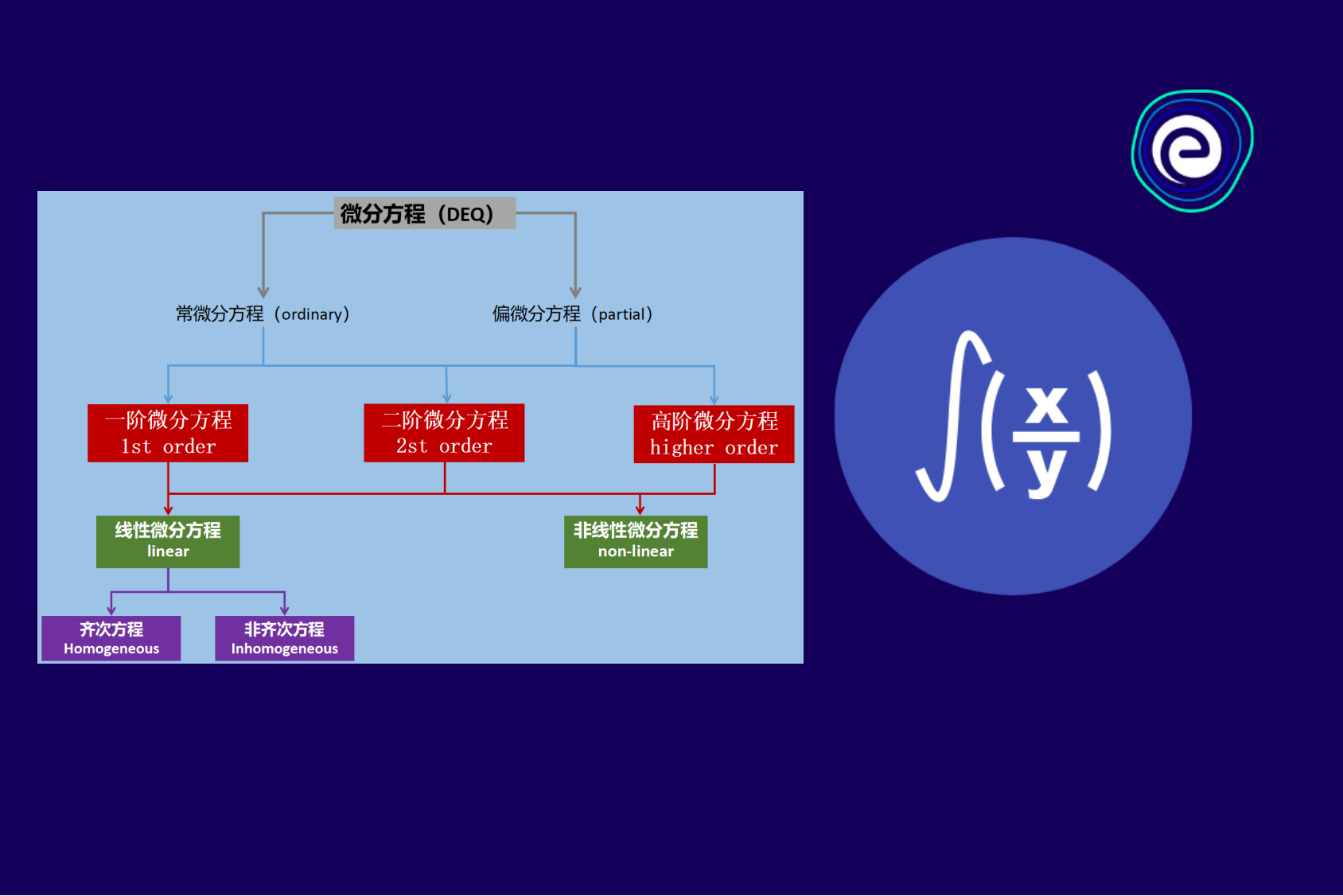
微分方程是数学的一个重要分支,广泛应用于物理、工程、经济等多个领域,用于描述众多的实际现象和问题。它们分为许多不同的类型,每种类型都有自己独特的性质和解法。理解这些分类可以帮助我们更好地理解微分方程的性质,从而更有效地求解微分方程。
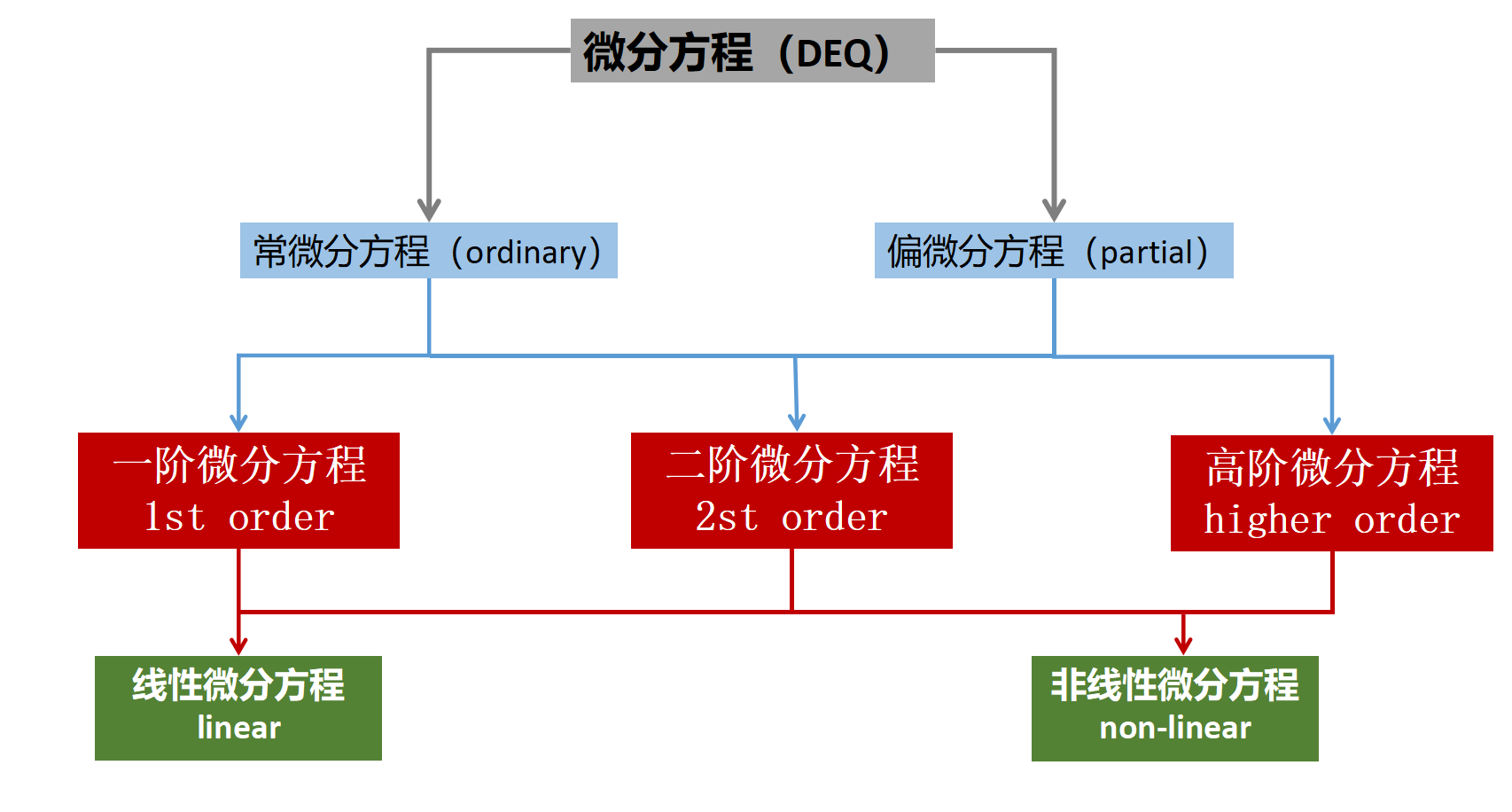
微分方程有常微分方程和偏微分方程。偏微分方程描述了多维问题,它们通常比较复杂。
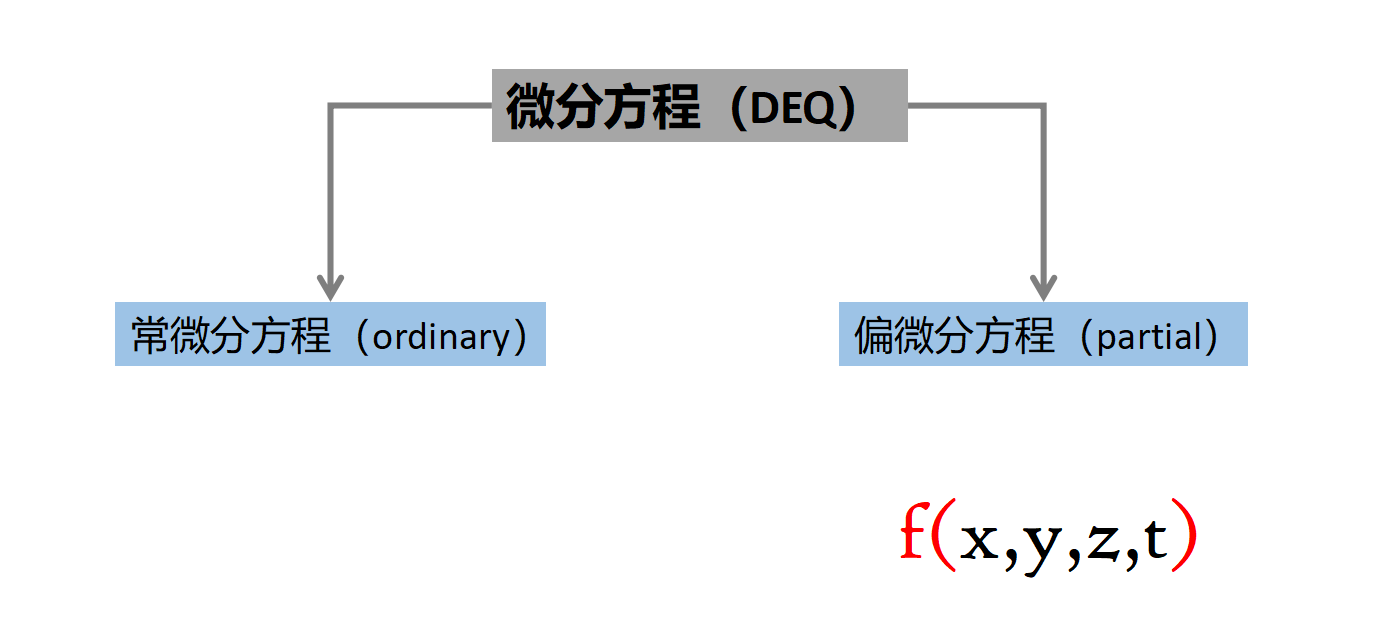
微分方程的阶数是多少?
第一阶微分方程通常容易解决,例如描述放射性衰变或液体冷却的行为。
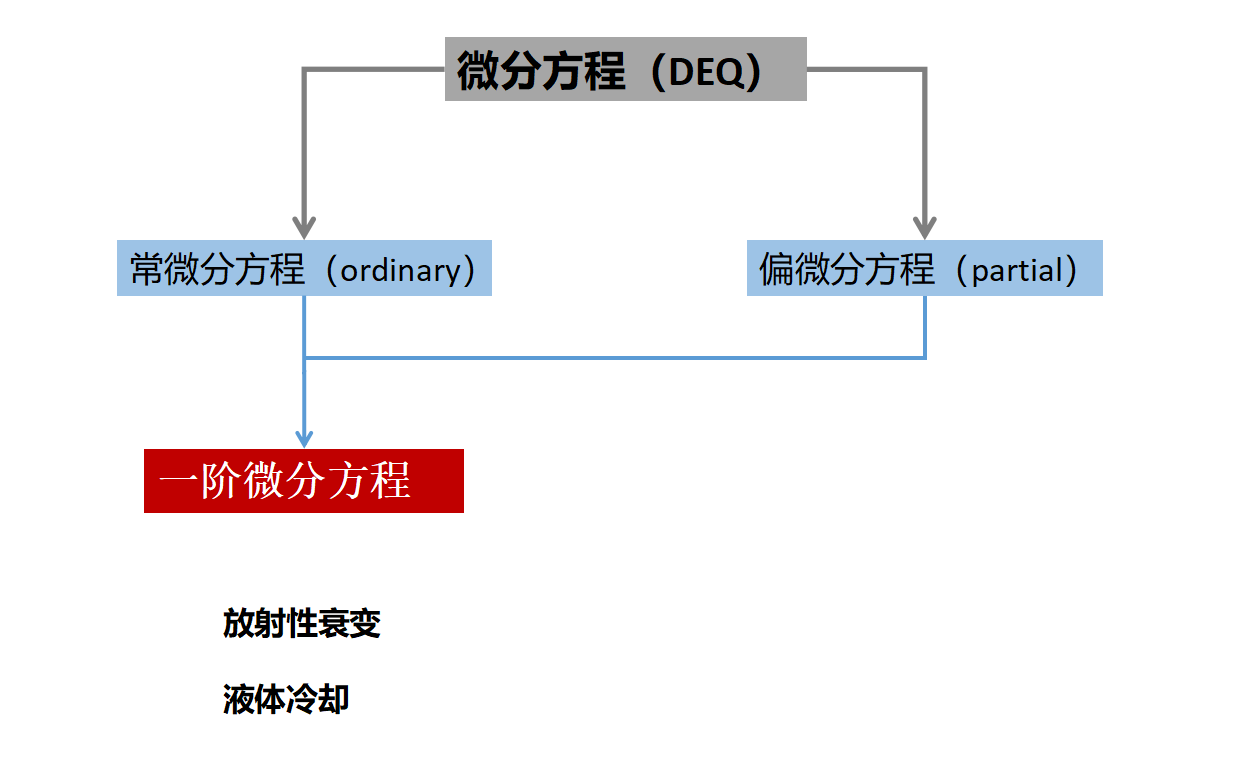
另一方面,二阶微分方程则相对复杂,也经常出现在自然界中。例如,电动力学的麦克斯韦方程,量子力学的薛定谔方程,都是二阶微分方程。只有从二阶开始,微分方程才能描述振动。而只有从三阶开始,微分方程才能描述混沌。
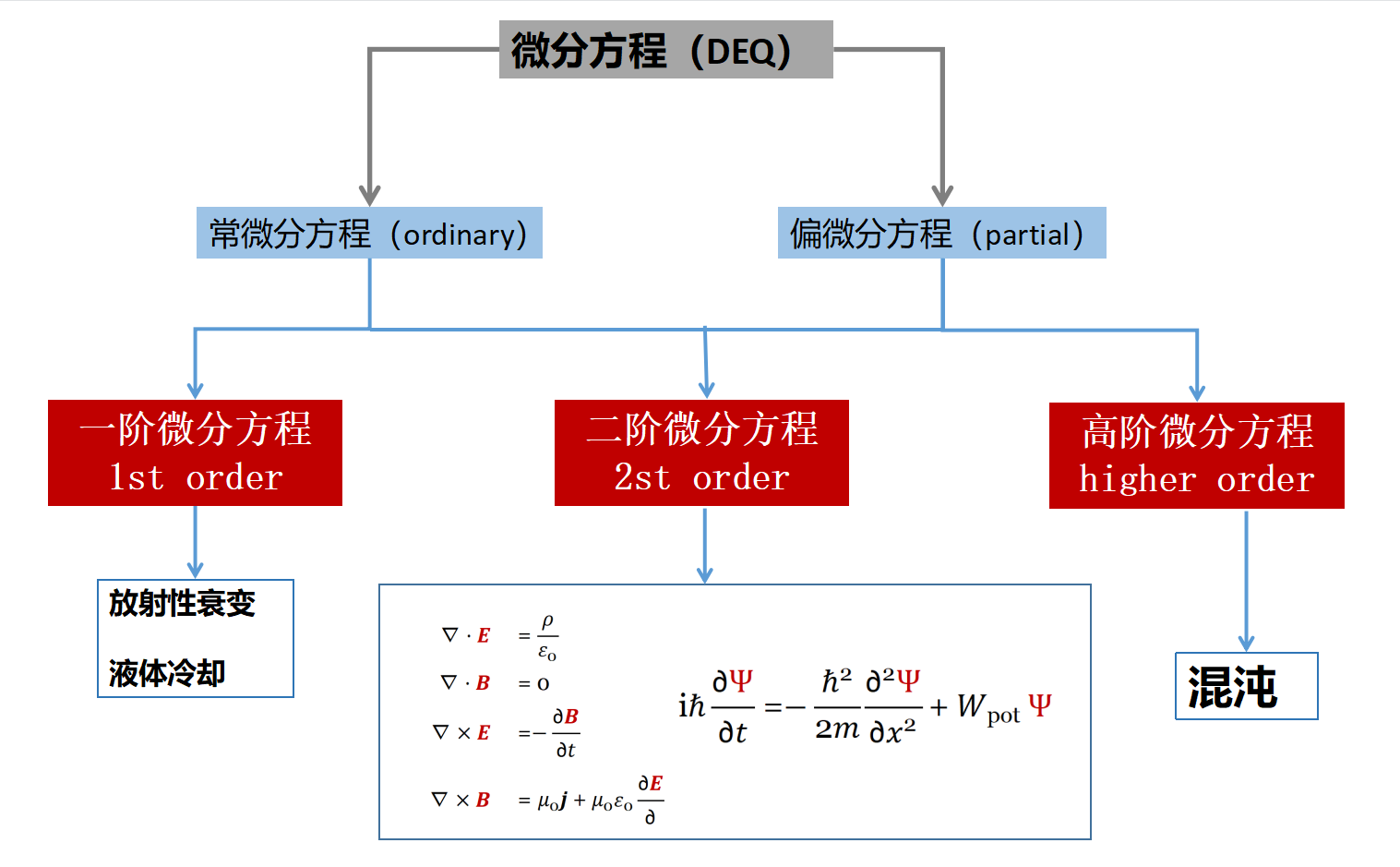
微分方程是线性的还是非线性的?
对于线性微分方程,有叠加原理,这在描述电磁现象时非常有用。非线性微分方程则更为复杂,例如在非线性电子学中描述超导电流时就会出现。
此外,只有在三阶及以上的非线性微分方程中才可能出现混沌。当你遇到这样的方程时,有时候唯一能做的就是放弃笔和纸,用计算机进行数值求解。许多非线性微分方程甚至无法进行解析求解,比如非常著名的纳维-斯托克斯方程。
线性微分方程是齐次的还是非齐次的?
齐次线性微分方程比非齐次的简单,例如,它可以描述未受扰动的振动,而非齐次微分方程则能描述受到外部扰动的振动。

首先,我们学习如何回答下面这些问题:

在你对微分方程进行分类后,你就可以具体地应用适当的方法来解这个方程。即使没有特定的求解方法,你也可以根据分类知道一个微分方程有多复杂。质量块的(非扰)振动方程是一个常(ordinar)微分方程,
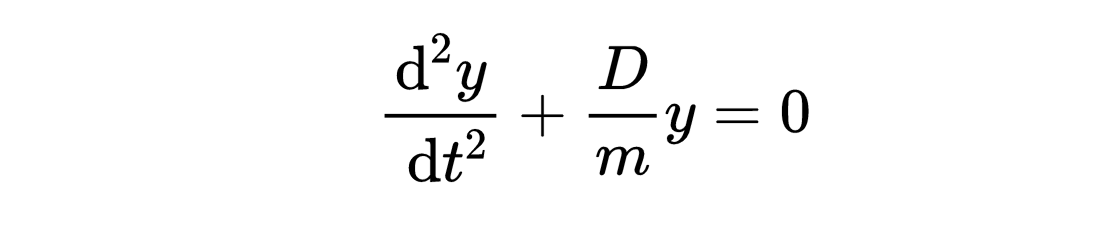
"常"意味着我们要寻找的函数y只依赖于一个变量,在这种情况下,是时间t。
什么是偏微分方程?波动方程则是一个偏(partial)微分方程,
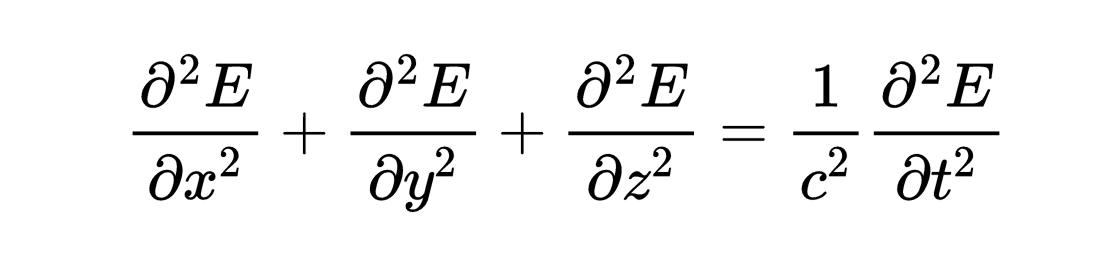
"偏"意味着要寻找的函数E至少依赖于两个变量,而这些变量的导数出现在方程中。在这个情况下,E依赖于四个变量:t,x,y 和 z。在微分方程中,也出现了对t,x,y,z的导数。
微分方程的阶是多少?此外,上面振动方程是二阶微分方程。微分方程的阶数是指函数的最高阶导数。因为振动方程中,y的最高阶导数是2,所以这是一个二阶微分方程。而放射性衰变定律的微分方程则是一阶的,
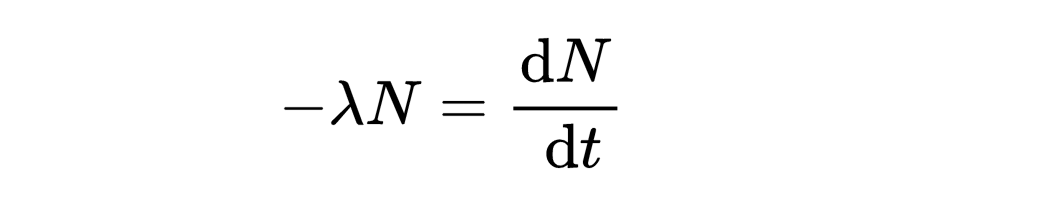
因为函数N的最高阶导数是一阶导数。
微分方程是线性的还是非线性的?此外,(非扰)振动方程是线性的。线性意味着要求的函数和它的导数的幂都是1,
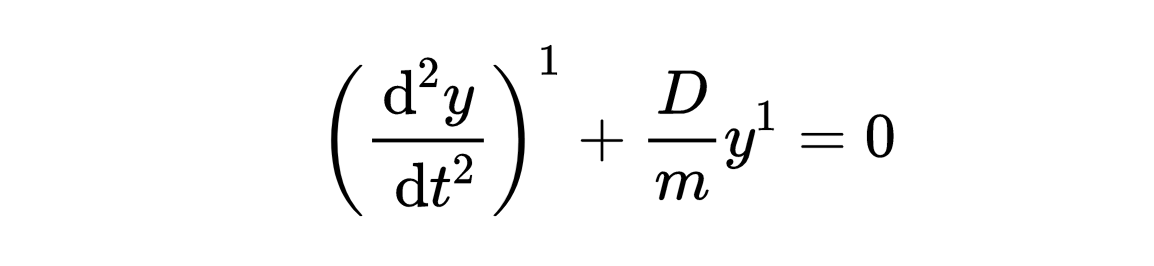
并且不包含导数和函数的乘积,如y^2或者y乘以y的二阶导数,

也不包含复合函数,如sin(y)或者y的平方根。需要注意的是,二阶导数中的'平方'在莱布尼茨符号中并不是导数的平方,而只是表示它是二阶导数。放射性衰变方程也是线性的,波动方程也是线性的。
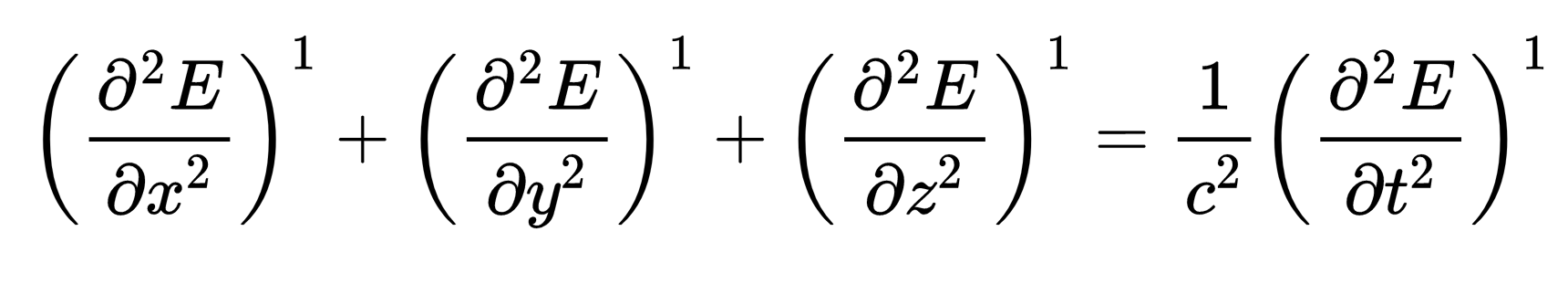
那什么是非线性微分方程呢?重力场中质量运动的耦合微分方程系统则是非线性的。
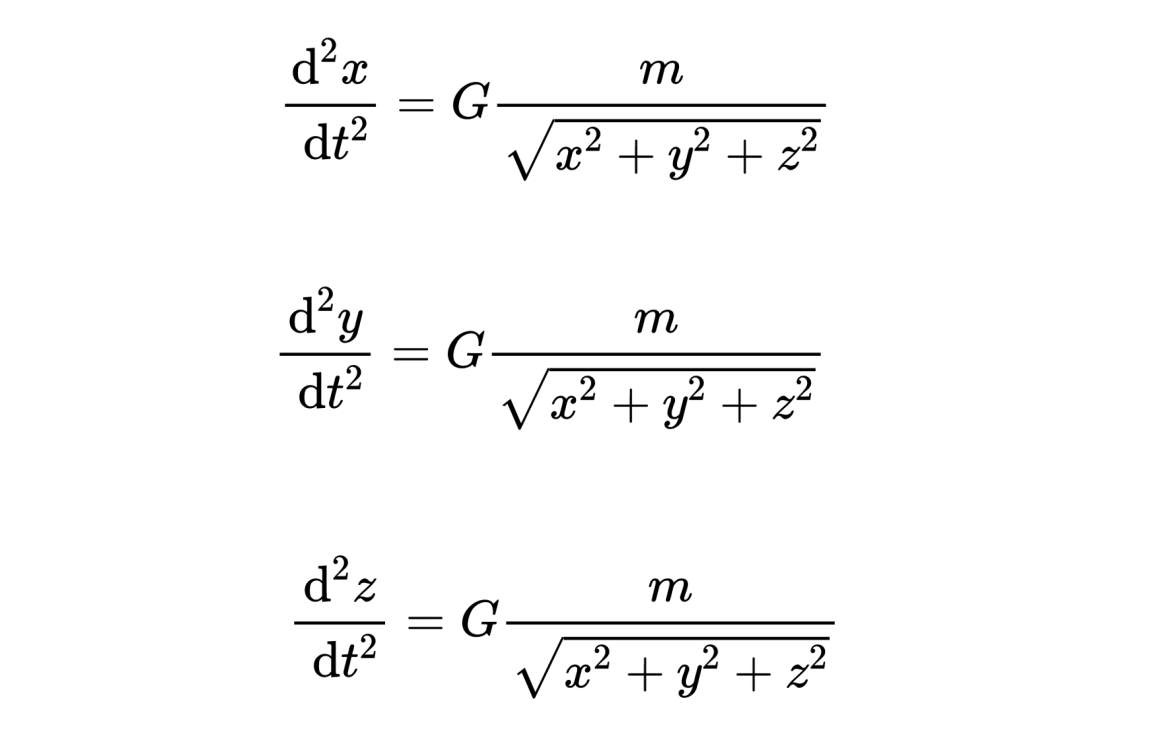
在这里,要求的函数x、y和z以二次形式出现。即使没有平方,方程中的平方根和分数也会使这个微分方程系统变为非线性!
在接下来的微分方程中,系数乘以被求函数及其导数是很重要的,在一些求解方法中,区分常数系数和非常数系数非常重要。

常数系数不依赖于(要被求的)函数所依赖的变量,非常数系数依赖于被求函数所依赖的变量。系数不一定要与被求函数或其导数相乘。它也可以单独存在!在这种情况下,我们称这个单一系数为扰动函数(perturbation function)。
在(非扰)振动微分方程中,
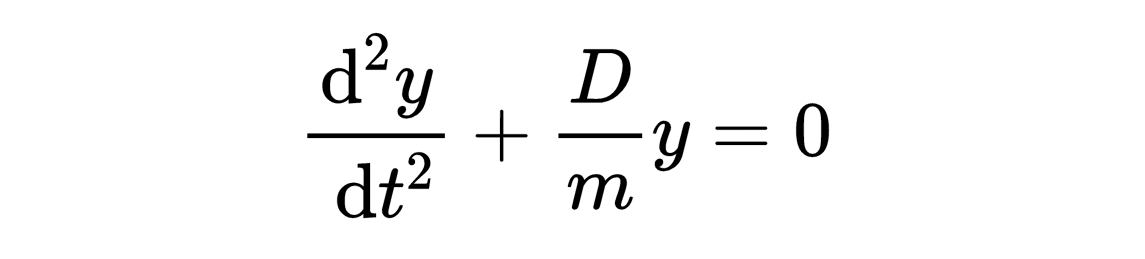
有一个常数系数乘以被求函数y,即D/m。严格来说,二阶导数前也有一个系数,即1,扰动函数在这里是0。
什么是齐次微分方程?如果扰动函数是零,那么我们称这个线性微分方程为齐次的。所以,振动微分方程是一个齐次微分方程。波动方程也是齐次的。因为扰动函数也是零。
那什么是非齐次微分方程呢?(受扰动)振动的微分方程则是非齐次的,
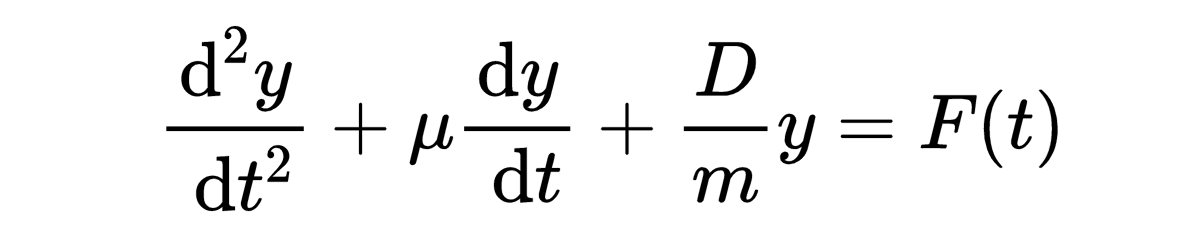
这里的外力F对应于扰动函数。此外,扰动函数F是时间依赖的,所以它是一个非常数系数。
