命题:若椭圆的焦点为
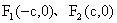
,离心率为
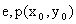
为椭圆上任意一点,则有
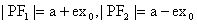
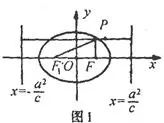
。证明:如图1,椭圆的准线方程为
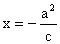
和
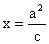
。由椭圆的第二定义得
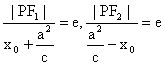
,化简即得说明:若椭圆的焦点在
轴上,则有
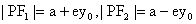
。我们把椭圆上的点到两焦点的距离
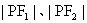
称为焦半径,而
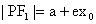
(或

)、
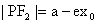
(或
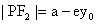
)称为焦半径公式。
巧用焦半径公式能妙解许多问题,下面举例说明。
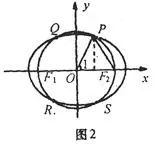
一、用于求离心率例1如图
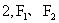
为椭圆的两个焦点,以线段为直径的圆交椭圆于
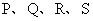
四点,顺次连结这四点和两个焦点,恰好围成一个正六边形,则离心率

。分析:如图,连
,则
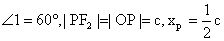
,由焦半径公式得
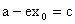
,即
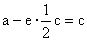
。所以
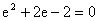
,所以
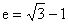
。
二、用于求椭圆离心率
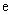
的取值范围例2已知为椭圆的焦点,若椭圆上恒存在点,使,求离心率的取值范围。分析:设的坐标为
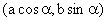
,则

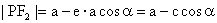
由得
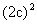
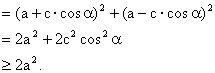
故
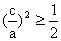
,即
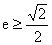
,又
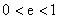
。所以
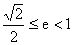
。 三、用于求焦半径的取值范围例3若是椭圆

上的点,为椭圆的焦点,求
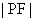
的取值范围。分析:不妨设为椭圆的左焦点,而
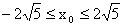
,则
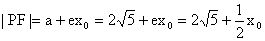
。故
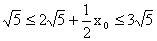
。所以
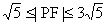
。 四、用于求两焦半径之积
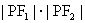
的最值例4若为椭圆
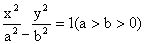
的左、右焦点,为椭圆上任意一点,求的最值。分析:易知
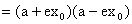
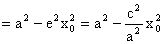
由
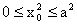
知
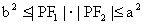
,所以的最小值为
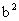
,最大值为
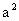
。 五、用于求三角形的面积例5 若是椭圆
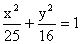
上一点,为椭圆的左、右焦点,且
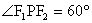
,求
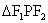
的面积S。分析:易知
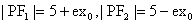
。由余弦定理得
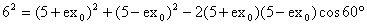
。解得
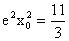
。所以

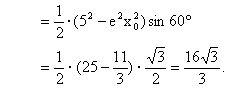
六、用于求点的坐标例6 若为椭圆
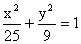
上的点,为椭圆的焦点,且,则的横坐标为_________。分析:由
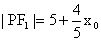
,
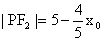
及得
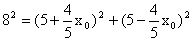
,解得
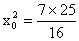
,所以
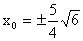
。 七、用于证明定值问题例7已知
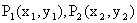
为椭圆上两点,
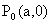
为椭圆的顶点,F为焦点,若
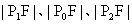
成等差数列,求证:
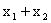
为定值。分析:不妨设
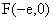
,由成等差数列得
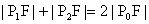
,即
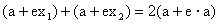
。化简得
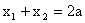
,
所以为定值。
八、用于求角的大小例8 如图3,设椭圆
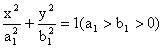
与双曲线
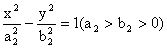
有公共焦点,为其交点,求
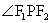
。
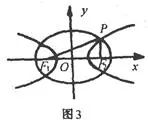
分析:设的坐标为
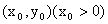
,椭圆与双曲线的离心率分别为
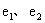
,则
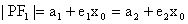
,
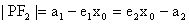
,消去
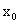
得

,
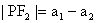
。所以
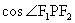
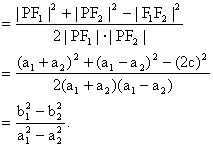
所以
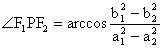
。 九、用于求线段的比。例9过椭圆
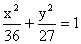
的左焦点作与长轴不垂直的弦
的垂直平分线交
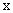
轴于
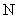
,则
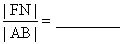
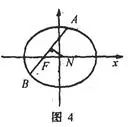
。分析:如图4,设
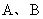
的坐标分别为
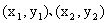
,AB的中点为

,则
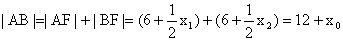
。
由
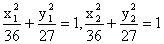
两式相减并化简得
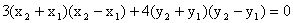
。
所以
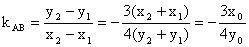
。
所以AB的垂直平行线方程为
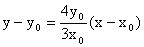
。令
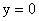
,则

,故N的坐标为
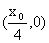
所以
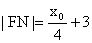
,所以
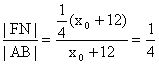
。
