说到数学爱情故事,首先就不得不提到广为流传的笛卡尔和他的心形线。
笛卡尔于1596年出生在法国,欧洲大陆爆发黑死病时他流浪到瑞典。
1650年,斯德哥尔摩的街头,52岁的笛卡尔邂逅了18岁的瑞典公主克里斯汀。后意外地接到通知,国王聘请他做公主的数学老师,日日相处使他们彼此产生爱慕之心,一段纯粹、美好的爱情悄然萌发。可是当他们的爱情传到国王耳朵里时,国王勃然大怒,下令将笛卡尔处死,后因公主求情将其流放回法国,克里斯汀公主也被父亲软禁起来
笛卡尔回法国后不久便染上黑死病,他日日给公主写信,因被国王拦截,克里斯汀一直没收到笛卡尔的信。笛卡尔在给克里斯汀寄出第十三封信后就气绝身亡了,这第十三封信内容只有短短的一个公式:r=a(1-sinθ)。
国王看不懂,觉得他们俩之间并不是总是说情话的,大发慈悲就把这封信交给一直闷闷不乐的克里斯汀,公主看到后,立即明了恋人的意图,她马上着手把方程的图形画出来,看到图形,她开心极了,她知道恋人仍然爱着她,原来方程的图形是一颗心的形状。公主在纸上建立了极坐标系,用笔在上面描下方程的点,看到了方程所表示的心脏线,理解了笛卡尔对自己的深深爱意。
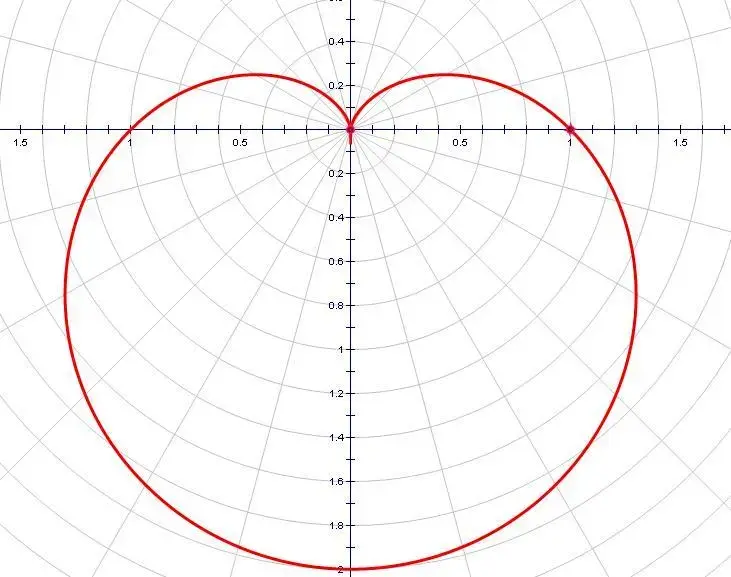
这也就是著名的“心形线”。

当然,过于浪漫的故事可能真的只是一个故事,无论故事杜撰与否,这个数学公式体情书也是极尽浪漫:r=a(1-sinθ)

用数学图形来表达爱情的例子还不止于此,再比如:莫比乌斯带。
莫比乌斯带由德国数学家莫比乌斯(Mobius,1790~1868)和约翰·李斯丁于1858年发现。就是把一根纸条扭转180°后,两头再粘接起来做成的纸带圈,具有魔术般的性质。
普通纸带具有两个面(即双侧曲面),一个正面,一个反面,两个面可以涂成不同的颜色;而这样的纸带只有一个面(即单侧曲面),一只小虫可以爬遍整个曲面而不必跨过它的边缘。这种纸带被称为“莫比乌斯带”(也就是说,它的曲面从两个减少到只有一个)。
莫比乌斯带是一种拓展图形,它们在图形被弯曲、拉大、缩小或任意的变形下保持不变,只要在变形过程中不使原来不同的点重合为同一个点,又不产生新点。
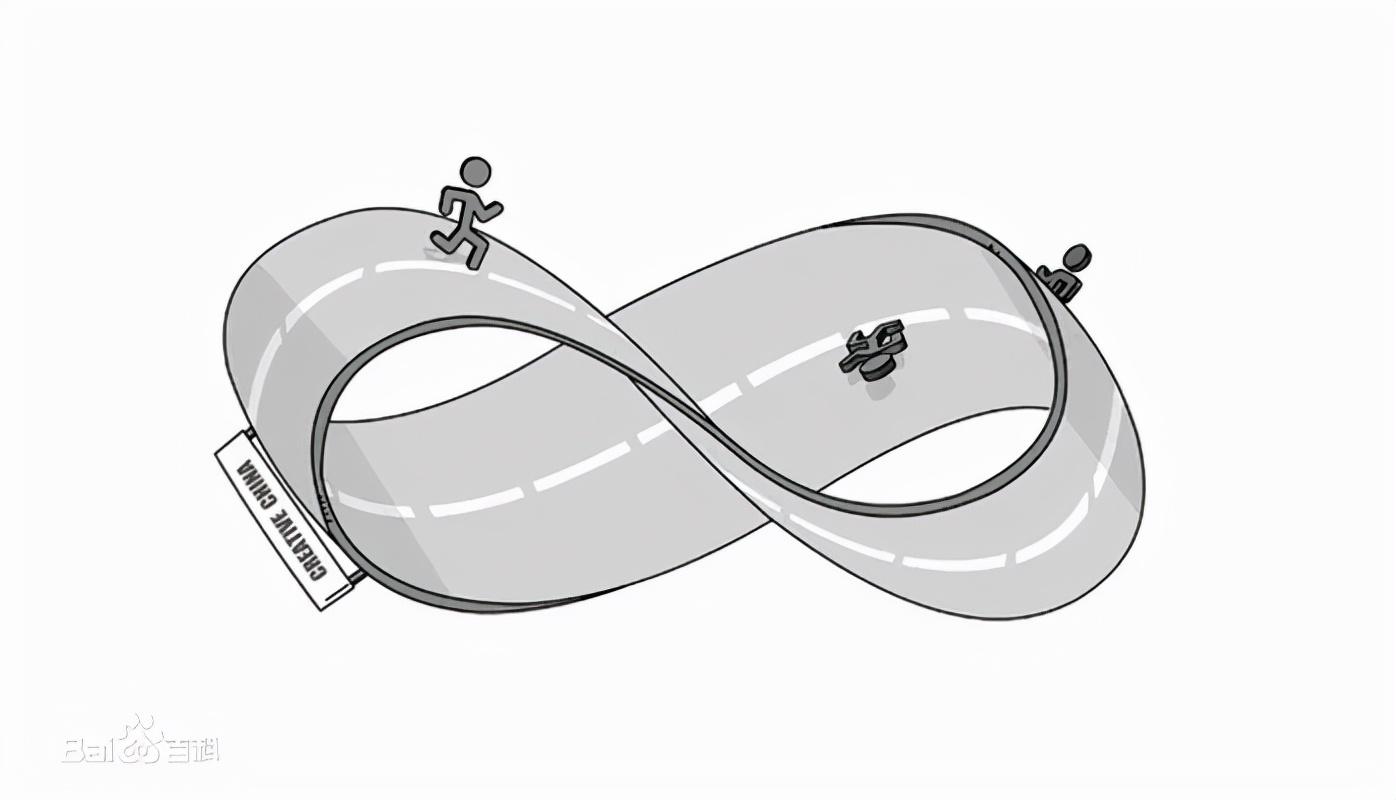
因为是循环往复的,所以莫比乌斯环又被赋予永恒和无限的含义。因此,一些人也通常用莫比乌斯环来比喻爱情的深远、循环和永恒。
有人说数学只是陈述客观事实,所有除数学之外的意义都是人为附加上去的。但是在尊重其数学意义的基础上,赋予它一些美好的意义,也未尝不可。毕竟,让枯燥的学术变得有趣,让更多人去了解它,不是更好吗?

下面整理了一些有趣的数学情诗,来一起感受下数学的罗曼蒂克。
01
我对你的思念就是一个循环小数,
一遍一遍,
执迷不悟。
02
零向量可以有很多方向,
却只有一个长度,
就像我,
可以有很多朋友,
却只有一个你,
值得我来守护。
03
如果我的心是x轴,
那你就是开口向上、
Δ为负的抛物线,
永远都在我的心上。
04
我每天带给你的惊喜和希望,
就像一个无穷集合里的每个元素,
虽然取之不尽,
却又各不一样。
05
如果你的心是x轴,
那我就是个正弦函数,
围你转动,
有收有放。
06
我对你的感情,
就像以自然对数e为底的指数函数,
不论经过多少求导的风雨,
依然不改本色,
真情永驻。
07
如果有一天我们分居异面直线的两头,
那我一定穿越时空的阻隔,
划条公垂线向你冲来,一刻也不愿逗留。
但如果有一天,
我们不幸被上帝扔到数轴的两端,
正负无穷,
生死相断,
没有关系,
只要求个倒数,
我们就能心心相依,
永远相伴
